Which of the following factors is not a distribution intermediary?
a.
Agent and broker
b.
Retailer
c.
Consumer
d.
Wholesaler
Answers
Answer:
c.
Consumer.............
As a consumer are the customers who receive the final product, we usually buy from the distributors. Agent and broker, retailers and wholesalers are the ones that distribute the product/ service to the consumer. They are the ones who sell the product/services e.g shops, supermarkets that sell in bulk, those who sell/market houses.
Hope this explanation helps.
Could you please mark as a brainliest (crown) above my comment. I’d appreciate it a lot.
Related Questions
A student was asked to give the exact solution to the equation
22x+4-9(2) = 0
The student's attempt is shown below:
22x+49(2)=0
22x+24-9(2) = 0
Let 2* = y
y²-9y+8=0
(y-8)(y-1)=0
y = 8 or y=1
So x = 3 or x = 0
(a) Identify the two errors made by the student.
(b) Find the exact solution to the equation.
Answers
(a) The errors made by the student are:
Incorrectly expanding 49(2) as 24 instead of 98.
Mistakenly factoring the quadratic equation as (y - 8)(y - 1) instead of
\(y^{2} - 9y + 8.\)
(b) The exact solution to the equation is x = 7/11.
(a) The student made two errors in their solution:
Error 1: In the step \("22x + 49(2) = 0,"\) the student incorrectly expanded 49(2) as 24 instead of 98. The correct expansion should be 49(2) = 98.
Error 2: In the step \("y^{2} - 9y + 8 = 0,"\) the student mistakenly factored the quadratic equation as (y - 8)(y - 1) = 0. The correct factorization should be \((y - 8)(y - 1) = y^{2} - 9y + 8.\)
(b) To find the exact solution to the equation, let's correct the errors made by the student and solve the equation:
Starting with the original equation: \(22x + 4 - 9(2) = 0\)
Simplifying: 22x + 4 - 18 = 0
Combining like terms: 22x - 14 = 0
Adding 14 to both sides: 22x = 14
Dividing both sides by 22: x = 14/22
Simplifying the fraction: x = 7/11
Therefore, the exact solution to the equation is x = 7/11.
For more questions on quadratic equation
https://brainly.com/question/30164833
#SPJ8
Help??
Anyone??
Need it in 3 min
7th grade math

Answers
Answer:
4.24 inches
Step-by-step explanation:
212/50
Answer:
4.24 inches
Step-by-step explanation:
To get the answer you divide 212 miles by 50 miles.
If η. is an even positive integer, the double factorial notation represents the product of all the even integers from to η. For example 8! = 2 . 4. 6. 8 . What is the units digit of the following sum?
a. 0
b. 2
c. 4
d. 6
e. 8
Answers
The units digit of the double factorial notation is the units digit of the product of all the even integers from 2 to 8, which is 8! The units digit of 8! is 8, so the answer is 8.
What is meant by the term factorials?Factorials are mathematical operations symbolized by an exclamation point following a number. To find the factorial of a number, such as 5, write it down as 5! then multiply it by all the positive integers less than 5, including 1. Therefore, 5! is equivalent to 5 x 4 x 3 x 2 x 1, or 120. Factorials are frequently employed in mathematical equations and computations, especially in probability and statistics, where they are used to calculate the number of combinations or permutations that may be made from a given collection of numbers or variables. For example, if you had 5 distinct objects and want to determine how many various combinations , you used the factorial of 5.
To learn more about factorials, visit:
https://brainly.com/question/1216161
#SPJ4
please help and add steps!!!!
i’m stuck :(

Answers
Answer:
09kikgjj78nmi
:
Find the domain and range of the function graphed below. Write your answers in interval notation.

Answers
Answer:
Domain: [-1, 3)
Range: (-5, 4]
LCM of 9 18 and 99 is :
Answers
Step-by-step explanation:
\(\begin{array}{c|ccc}\cline {2-4} 2 & 9 ,& 18 ,& 99 \\ \cline {2-4} 3 & 9 & ,9 & ,11 \\ \cline {2-4} 3 & 3 ,& 3, & 11 \\ & 1, & 1 , & 11 \end {array}\)
LCM=2×3×3×11=198There are 95 students at an
assembly. They are sitting in rows
and there are 7 students in each
row. How many rows will be needed
to seat all the students?
Answers
95 divided by 7 is 13.57 so Round up to 14.
Answer:
about 14 chairs
Step-by-step explanation:
All you do is do 95 divided by 7, which is 13.57142857142857.... If your teacher would want you to round, then answer with 14, but if they wouldn't, I would just do 14
“solve the following equations using substitution please show all your work”pleas help i don’t understand how to solve

Answers
Explanation
We are given the following:
\(\begin{gathered} 4x-3y=10\text{ \lparen equation 1\rparen} \\ 4x-2y=3\text{ \lparen equation 2\rparen} \end{gathered}\)We are required to solve the simultaneous equation given using substitution method.
This can be achieved as follows:
\(\begin{gathered} \text{ From equation 1, } \\ 4x-3y=10 \\ 4x=10+3y\text{ \lparen equation 3\rparen} \\ \\ \text{ Substitute for ''4x'' in equation 2.} \\ 4x-2y=3 \\ (10+3y)-2y=3 \\ 10+3y-2y=3 \\ 3y-2y=3-10 \\ y=-7 \end{gathered}\)Now, we get the value of x as follows:
\(\begin{gathered} \text{ From equation 3} \\ 4x=10+3y \\ where \\ y=-7 \\ 4x=10+3(-7) \\ 4x=10-21 \\ 4x=-11 \\ x=\frac{-11}{4} \end{gathered}\)Hence, the answer is:
\(x=\frac{-11}{4};y=-7\)If DE =11 and CE =27, what is CD?

Answers
Answer:
16
Step-by-step explanation:
Subtract DE from CE and you will get the value of CD
27 - 11 = 16
A is thrice as good as workman as B and therefore is able to finish a job in 60 days less than B. Working together, they can do it in
20.4 days
22.5 days
25.6 days
30.1 days
Answers
Let's assume that B can do the job alone in x days.
Then, according to the question, A can do the same job alone in (1/3)x days.
Also, we know that A takes 60 days less than B to finish the job, so:
(1/3)x = x - 60
Solving for x, we get:
x = 90
Therefore, B can do the job alone in 90 days and A can do the same job alone in (1/3) * 90 = 30 days.
To find out how long they take to finish the job together, we use the formula:
(AB)/ (A+B)
where AB is the product of their individual times and A+B is their combined time.
Plugging in the values, we get:
(30 * 90)/(30+90) = 22.5
Therefore, working together, they can finish the job in 22.5 days.
Answer: Option B - 22.5 days
Does anyone know these?

Answers
Answer:
1 = - 4 - 14 √3
2 = 9 - 11 √3
Step-by-step explanation:
Question 1
(-4√3 + 2)(√3 + 4)
Apply FOIL method
= (-4√3) √3 + (-4√3) . 4 + 2 √3 + 2 . 4
Apply minus-plus rules: + (-a) = -a
= -4 √3 √3 - 4 . 4 √3 + 2 √3 + 2 . 4
Simplify
= - 4 - 14 √3
Question 2
(-3 + √3)(1 + 4 √3)
Apply FOIL method
= (-3) . 1 + (-3) . 4 √3 + √3 . 1 + √3 . 4 √3
Apply minus-plus rules: + (-a) = -a
= -3 . 1 - 3 . 4 √3 + 1 . √3 + 4 √3 √3
Simplify
= 9 - 11 √3
King of Diamonds Industries has bonds on the market making annual payments, with 14 years to maturity, and selling for R1 482,01. At this price, the bonds yield 7%. What is the coupon rate?
Answers
The coupon rate of the bonds by King of Diamonds Industries would be 7 %.
How to find the coupon rate ?The formula for the bond price shows the coupon payment and so can be used to find the coupon rate:
= (Coupon payment x ( 1 - ( 1 + r ) ^ ( - number of years till maturity ) ) ) / r + Face value / (1 + rate )^ number of years
1,482.01 = (C x (1 - (1 + 0.07 )^ (- 14) ) ) / 0.07 + F / (1 + 0.07 ) ^ 14
103.7407 - 0.07 x (F / (1 + 0.07) ^14 ) = C x (1 - ( 1 + 0.07) ^ ( - 14) )
Using a calculator, C is $ 70.
This means that the coupon rate is:
= 70 / 1, 000
= 7 %
Find out more on the coupon rate at https://brainly.com/question/28528712
#SPJ1
What is the range of this data set?

Answers
Answer:
The Range = 72
Step-by-step explanation:
Definition ==================================
The Range of data set is is the difference between the smallest and largest values
……………………………………………………………
The Range = 78 - 6 = 72
A system of equations and its solution are given below. System A x + 6 y = 5 3 x − 7 y = − 35 Solution: ( − 7 , 2 ) Choose the correct option that explains what steps were followed to obtain the system of equations below. System B x + 6 y = 5 − 25 y = − 50 A. To get system B, the second equation in system A was replaced by the sum of that equation and the first equation multiplied by -3. The solution to system B will be the same as the solution to system A. B. To get system B, the second equation in system A was replaced by the sum of that equation and the first equation multiplied by 3. The solution to system B will not be the same as the solution to system A. C. To get system B, the second equation in system A was replaced by the sum of that equation and the first equation multiplied by 7. The solution to system B will not be the same as the solution to system A. D. To get system B, the second equation in system A was replaced by the sum of that equation and the first equation multiplied by -5. The solution to system B will be the same as the solution to system A.
Answers
To get system B, the second equation in system A was replaced by the sum of that equation and the first equation multiplied by -3. The solution to system B will be the same as the solution to system A.
What is Linear equation ?
Linear equation can be defined as the equation in which the highest degree is one.
First equation of system A multiplied by -3:
(-3)(x+6y=5)
(-3)(x)+(-3)(6)=(-3)(5)
-3x-18=-15
Sum of the second equation of system A and the first equation multiplied by -3:
(-3x-18)+(3x-7y)=(-15)+(-35)
-3x-18+3x-7y=-15-35
-25y=-50
System B
x+6y=5
-25y=-50
Hence, To get system B, the second equation in system A was replaced by the sum of that equation and the first equation multiplied by -3. The solution to system B will be the same as the solution to system A.
To learn more about Linear Equation from the given link.
brainly.com/question/29739212
#SPJ1
Suppose a charity event serves a prix fixe dinner that consists of one from each category: (1) soup or salad (not both), (2) appetizer, (3) entree, (4) dessert, and (5) beverage. The restaurant is offering five kinds of soup, three kinds of salad, four kinds of appetizers, six entrees, five desserts, and four beverages. How many different prix fixe dinners are possible
Answers
Answer:
3840
Step-by-step explanation:
Using the fundamental counting principle
The restaurant is offering five kinds of soup, three kinds of salad, four kinds of appetizers, six entrees, five desserts, and four beverages.
There are 5 independent events happening (5 prixe dinners)
(1) soup or salad (not both)
We have five kinds of soup, three kinds of salad
soup or salad (not both), = 5 + 3
= 8
(2) appetizer = 4
(3) entrees = 6
(4) dessert = 5
(5) Beverage = 4
Hence,
8 × 4 × 6 × 5 × 4
= 3840
The number of different prix fixe dinners are possible is 3840
A number cube numbered 1-6 is rolled 30 times and lands on an even number 18 times.
How does this frequency compare to the expected frequency based on the probability of
the number cube landing on an even number?
The frequency is 15 more than expected.
The frequency is 13 more than expected.
The frequency is 9 more than expected.
The frequency is 3 more than expected.
Done →
Answers
Given statement solution is :- The correct answer is: The frequency is 3 more than expected.
To determine the expected frequency of landing on an even number when rolling a fair six-sided number cube, we need to calculate the probability of landing on an even number and multiply it by the total number of rolls.
The number cube has six possible outcomes: 1, 2, 3, 4, 5, and 6. Of these, three are even numbers: 2, 4, and 6. Therefore, the probability of rolling an even number is 3/6, which simplifies to 1/2 or 0.5.
The expected frequency can be found by multiplying the probability by the total number of rolls:
Expected frequency = Probability of landing on an even number × Total number of rolls
Expected frequency = 0.5 × 30 = 15
Now, we can compare the expected frequency (15) to the actual frequency (18) given in the problem statement.
The actual frequency is 18, and it is 3 more than the expected frequency (18 - 15 = 3).
Therefore, the correct answer is: The frequency is 3 more than expected.
For such more questions on Frequency Difference
https://brainly.com/question/13193436
#SPJ8
Given: LM ∥ KN
LP ⊥ KN , KL = MN
KN = 30, LM = 20
m∠KLM=126°
Find: LP
Answers
An angle is produced at the point where two or more lines meet. Thus the value of LP required in the question is approximately 14.
Two lines are said to be perpendicular when a measure of the angle between them is a right angle. While parallel lines are lines that do not meet even when extended to infinity.
From the question, let the length of LP be represented by x.
Thus, from the given question, it can be deduced that;
LM ≅ PN = 20
KP = KN - PN
= 30 - 20
KP = 10
LP = x
Also,
<MLP is a right angle, so that;
< KLP = < KLM - <PLM
= 126 - 90
<KLP = \(36^{o}\)
So that applying the Pythagoras theorem to triangle KLP, we have;
Tan θ = \(\frac{opposite}{adjacent}\)
Tan 36 = \(\frac{10}{x}\)
x = \(\frac{10}{Tan 36}\)
= \(\frac{10}{0.7265}\)
x = 13.765
Therefore the side LP ≅ 14.
For more clarifications on segments and angles, visit: https://brainly.com/question/4976881
#SPJ1

can someone please solve and explain how you got your answer, WILL GIVE BRAINLIEST!!!

Answers
Answer:
A, graph 4, S(0, 9)B, graph 3, R(9, 0)C, graph 1, P(3, 9)D, graph 2, Q(-3, 0)Step-by-step explanation:
You want to identify the graphs that go with each of these functions, along with a particular point on the curve.
y = x² +3x +9y = (x +3)(x -9)y = (x -3)² +9y = -(x -9)(x +3)Quadratic features of interestThe equations are written here in standard form, factored form, and vertex form. (The "factored form" is sometimes called "intercept form.") Each of these forms can be analyzed for characteristics relevant to identifying the corresponding graph.
In general, we can readily identify the opening direction, based on the sign of the leading coefficient. Depending on the form, we can also identify zeros, the vertex, and the y-intercept.
Standard formThe line of symmetry (x-coordinate of the vertex) of the equation in the form ax² +bx +c is x = -b/(2a). That is, it will be left of the y-axis when the coefficients 'a' and 'b' have the same sign.
The graph of equation A will be graph 4, the only one with its vertex left of the y-axis. The y-intercept is the constant: point S = (0, 9).
Factored formEquation B has a positive leading coefficient, so opens upward. The zeros of the factors are -3 and +9, so identify the places where the graph crosses the x-axis. Graph 3 is the only one that opens upward and has x-intercepts. Point R is (9, 0).
Vertex formThe vertex form of a quadratic is ...
y = a(x -h)² +k . . . . . . . vertex (h, k); leading coefficient 'a'
Equation C has its vertex at (h, k) = (3, 9) and opens upward (a>0). Graph 1 is the only one matching those characteristics. Point P is the vertex, so point P is (3, 9).
Leading coefficientEquation D is the same as equation B, but with a negative leading coefficient. That is, it opens downward and crosses the x-axis in two places, at x = -3 and x = 9. Graph 2 is matches this description. The left zero is point Q, (-3, 0).
<95141404393>
find the area of the circle which is circumscribed about the right triangle with legs 6 and 8
Answers
The area of the circle circumscribed about the right triangle with legs 6 and 8 is approximately 78.54 square units.
To find the area of the circle circumscribed about a right triangle, we can use the fact that the diameter of the circle is equal to the hypotenuse of the right triangle. In this case, the legs of the right triangle are given as 6 and 8.
Using the Pythagorean theorem, we can find the length of the hypotenuse:
\(c^2 = a^2 + b^2\)
where c is the length of the hypotenuse, and a and b are the lengths of the legs.
Substituting the values:
\(c^2 = 6^2 + 8^2\)
\(c^2 = 36 + 64\\ c^2 = 100\)
Taking the square root of both sides:
\(c = \sqrt{100} \\ c = 10\)
Therefore, the length of the hypotenuse is 10 units.
Since the diameter of the circumscribed circle is equal to the hypotenuse, the radius of the circle is half the length of the hypotenuse, which is 10/2 = 5 units.
Now we can calculate the area of the circle using the formula:
Area = π \(r^2\)
where r is the radius of the circle.
Area = π \(5^2\)
Area = π × 25
Area = 78.54 square units
Hence, the area of the circle circumscribed about the right triangle with legs 6 and 8 is approximately 78.54 square units.
For more questions on area
https://brainly.com/question/22972014
#SPJ8
7. How many solutions does the given system have?
y = 3x + 1
6x - 2y = -2
A. one solution
B. two solutions
C. infinite solutions
D. no solution
Answers
Answer:
C infinite solutions
Step-by-step explanation:
First put both equations in the form of y=mx+b then you will get the same equation in both. Since both equations are the same they intersect at all the points which means this system has infinite solutions.

Someone help me please and thank you

Answers
Answer: 2a < 2b
Step-by-step explanation:
We are given a statement:
a < b and b < c, then 2a ____ 2b
We can use simple numbers that make the statement true.
Where,
a = 2
b = 3
c = 4
Now lets plug it in.
2 < 3 and 3 < 4, then 2(2) ____ 2(3)
and lets simplify:
2 < 3 and 3 < 4, then 4 ____ 6
We can see that 4 is less than 6,
so as a is less than b, 2a is less than 2b.
The only thing changing is the coefficient being multiplied by the variables a and b.
Suppose that, next month, the technology group will receive 24 requests for help with computer problems. Among, these, 19 are software related and 5 are hardware problems. If a novice in the group is randomly assign to 3 problems, what are the probabilities that she will address.
Answers
See below for the appropriate and correct question.
Suppose that, next month, the technology group will receive 24 requests for help with computer problems. Among, these, 19 are software related and 5 are hardware problems. If a novice in the group is randomly assigned to 3 problems, what are the probabilities that she will address:
a. none of the hardware problems?
b. only one of the hardware problems?
Answer:
a. the probabilities that she will address none of the hardware problems 0.4788
b. the probabilities that she will address only one of the hardware problems 0.4224
Step-by-step explanation:
From the information given:
Let represent R to be the total number of request received.
i.e. R = 24
Let the number of hardware problems be p = 5
Let the number of the randomly assigned problem be m = 3
Then, we can compute the probability mass function of a hypergeometric distribution by using the formula:
\(h(x,m,p,R) = \dfrac{ (^p_x) (^{R-p}_{m-x}) }{^R_m}\) where x can be 0,1,2,3...
Thus;
\(h(x,3,5,24) = \dfrac{ (^5_x) (^{24-5}_{3-x}) }{(^{24}_3)}\)
(a). To find the probability that she will address none of the hardware problems; we have:
x = 0
Then:
\(h(0;3,5,24) = \dfrac{ (^5_0) (^{24-5}_{3-0}) }{(^{24}_3)}\)
\(h(0;3,5,24) = \dfrac{ (^5_0) (^{19}_{3}) }{(^{24}_3)}\)
\(h(0;3,5,24) = \dfrac{ \dfrac{5!}{0!(5-0)!} \times \dfrac{19!}{3!(19-3)!} }{\dfrac{24!}{3!(24-3)!}}\)
\(h(0;3,5,24) = \dfrac{ 1 \times 969 }{2024}\)
\(h(0;3,5,24) = 0.4788\)
b) To find the probability that she will address only one of the hardware problems; we have:
x = 1
Then:
\(h(1;3,5,24) = \dfrac{ (^5_1) (^{24-5}_{3-1}) }{(^{24}_3)}\)
\(h(1;3,5,24) = \dfrac{ (^5_1) (^{19}_{2}) }{(^{24}_3)}\)
\(h(1;3,5,24) = \dfrac{ \dfrac{5!}{1!(5-1)!} \times \dfrac{19!}{2!(19-2)!} }{\dfrac{24!}{3!(24-3)!}}\)
\(h(1;3,5,24) = \dfrac{ 5 \times 171 }{2024}\)
\(h(1;3,5,24) = 0.4424\)
A job pays $10.00 an hour today.If the same percentage applies to income as well as bread {previous slide}, how much would that job have paid 1955
Answers
Answer:
67 cents
Step-by-step explanation:
Answer:
67 cents
Step-by-step explanation:
im smart
Write the equation of the line that passes through the points (-7,7) and (-6, -5)
Put your answer in fully reduced point-slope form, unless it is a vertical or horizontal
line.
Answers
Answer:
y = -12x -77
Step-by-step explanation:
-5 - -7/-6 - -7 = -12
slope = -12
y = mx + b
Subsutitue
7 = -12 ⋅ -7 + b
b = -77
good luck, i hope this helps :)
Forest Fires and Acres Burned Numbers (in thousands) of forest fires over the year and the number (in hundred thousands) of acres burned for 7 recent years are shown. Number of fires x 69 58 47 84 62 57 72 Number of acres burned y 64 53 42 79 57 52 67 The correlation coefficient for the data is r=1 and α=0.05. Should regression analysis be done? The regression analysis should not be done. The regression analysis should be done. Find the equation of the regression line. y′=a+bx a= Find y' when x=50
Answers
The equation of the regression line is y = 4 + x and the regression analysis of the given data need not be done.
Straight line equation is y = a + bx.
The normal equations are
∑y = a·n + b ∑x ∑ xy = a ∑x + b∑x² Hence the regression analysis of the data :
The values are calculated using the following table
x y x² x⋅y
58 62 3364 3596
47 51 2209 2397
84 88 7056 7392
62 66 3844 4092
57 61 3249 3477
72 76 5184 5472
69 73 4761 5037
hence :
∑x = 449
∑y = 477
∑x² = 29667
∑x⋅y = 31463
Substituting these values in the normal equations
7a+449b=477
449a+29667b=31463
Solving these two equations using Elimination method,
7a+449b=477
and 449a+29667b=31463
7a+449b=477→(1)
449a+29667b=31463→(2)
equation(1)×449
⇒3143a+201601b=214173
equation(2)×7
⇒3143a+207669b=220241
Substracting
⇒-6068b = -6068
⇒6068b = 6068
⇒b = 1
Putting b = 1 in equation (1), we have
7a+449(1) = 477
⇒7a = 477 - 449
⇒7a = 28 or a = 4.
Now Estimate y for x=50
y = a + bx , we get
y = 4 + 1×50
y = 4 + 50
y = 54
At x equals 50 we get the value of y as 54 .
To learn more about regression line visit:
https://brainly.com/question/7656407
#SPJ4
You can get 20 points or more if you help me with this problem and I will also vote you as the brainiest. But, your answer must be accurate so, please help.

Answers
Answer:
oi mate
for the 1st one its "it means that there are 36 cookies in 3 dozen"
for the 2nd one its"(1,12) since 1 is the start and 12 is the beginning
Step-by-step explanation:
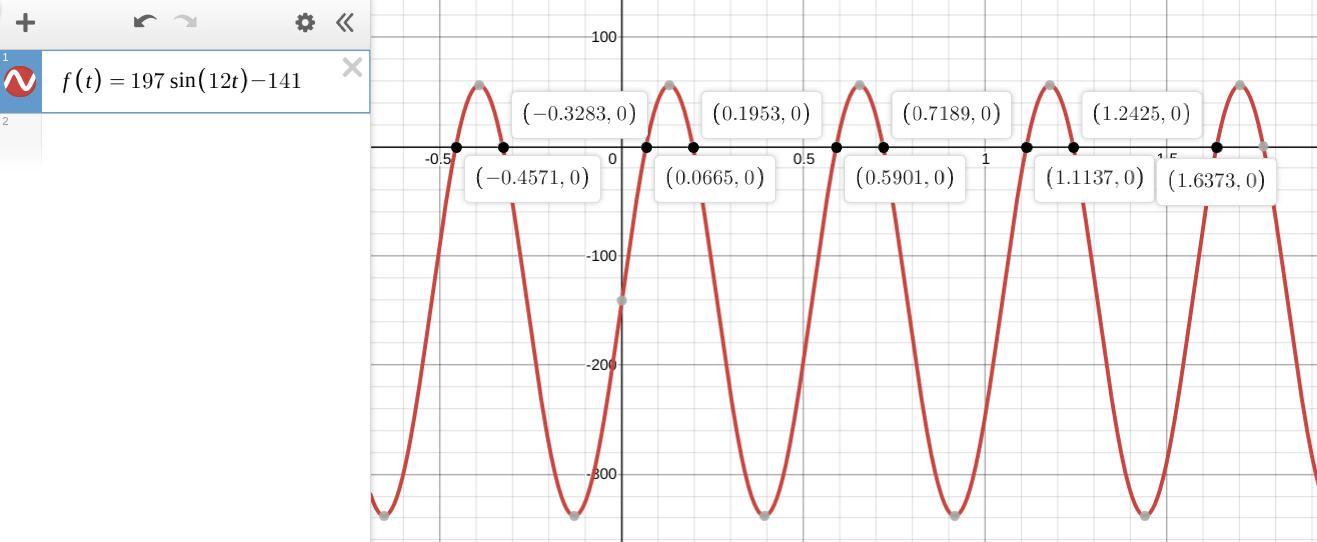
What is t in 197sin(12t)=141
Answers
Answer:
t ≈ 0.0664731
Step-by-step explanation:
Use the inverse sine function.
sin(12t) = 141/197
12t = arcsin(141/197)
t = arcsin(141/197)/12
t ≈ 0.0664731 . . . . . . . radians
__
This is the principal value. There are other solutions at values of t that have integer multiples of π/6 added to this. There are also solutions where any of those values is subtracted from π.
_____
In general, angles in math are assumed to be in radians, unless specified otherwise. This angle corresponds to about 3.81°. (In geometry, the usual assumption is that angles are measured in degrees.)
Isaiah scores with 50% of his penalty kicks in soccer. He flips two fair coins to conduct a simulation with 20 trials to determine the likelihood that he will make his next two penalty kicks, as shown. Heads up (H) represents a goal. What is the probability that Isaiah will make both penalty kicks? Give the probability as a percent. Enter your answer in the box. TH HH TT HT TH HH HH TT HT TH TT HH HT HH HH TT HT HH TH TT P(two goals) = %
Answers
The probability that Isaiah will make both penalty kicks, as simulated by flipping two fair coins 20 times, is 25%.
Since Isaiah scores with a 50% success rate on penalty kicks, the probability of him scoring a goal on any given penalty kick is 0.5 or 50%.
If he flips two fair coins to simulate 20 trials, there are four possible outcomes: HH (two goals), HT (one goal and one miss), TH (one goal and one miss), and TT (two misses).
Out of the 20 trials, there are two possible ways for Isaiah to score both of his penalty kicks: HH and HH. The probability of getting HH on two coin flips is (0.5) x (0.5) = 0.25 or 25%.
Therefore, the probability that Isaiah will make both penalty kicks, as simulated by flipping two fair coins 20 times, is 25%.
Expressed as a percentage, this is:
P(two goals) = 25%
for similar questions on probability
https://brainly.com/question/251701
#SPJ11
Please HELP!!!
Will give 15 points!!
For a test that’s due today!!

Answers
Answer:
A
Step-by-step explanation:
For a right triangle
\(A=\frac{ab}{2} \\\frac{(10.4)(15.3)}{2} =79.56\)
This is the same as the other triangle because they are the same size because of congruency
Area of the rectangle
\(a^2+b^2=c^2\\\)
\(\sqrt{(10.4^2+15.3^2} =c\)
\(c= 18.5\)
18.5 x 7 = 129.5
Add them all up
129.5+79.56+79.56= 288.62
components arriving at a distributor are checked for defects by two different inspectors (each component is checked by both inspectors). the first inspector detects 87% of all defectives that are present, and the second inspector does likewise. at least one inspector does not detect a defect on 26% of all defective components. what is the probability that the following occur?
Answers
The probability that a defective component will be detected only by the first inspector is 0.19
The probability that a defective component will be detected by exactly one of the two inspectors is 0.38
The probability that all three defective components in a batch escape detection by both inspectors is 0.
It is given that The first inspector detects 81% of all defectives that are present, and the second inspector does likewise.
Therefore P(A)=P(B)=81%=0.81
At least one inspector does not detect a defect on 38% of all defective components.
Therefore, bar P(A∩B)=0.38
As we know:
bar P(A∩B)=1-P(A∩B)=0.38
P(A∩B)=1-0.38=0.62
A defective component will be detected only by the first inspector.
P(A∩barB)=P(A)-P(A∩B)
=0.81-0.62
P(A∩barB)=0.19
The probability that a defective component will be detected only by the first inspector is 0.19
Part (B) A defective component will be detected by exactly one of the two inspectors.
This can be written as: P(A∩barB)+P(barA∩B)
As we know:
P(barA∩B)=P(B)-P(A∩B) and P(A∩bar B)=P(A)-P(A∩B)
Substitute the respective values we get:
P(A∩ barB)+P(bar A∩B)=P(A)+P(B)-2P(A∩B)
=0.81+0.81-2(0.62)
=1.62-1.24
P(A∩ barB)+P(bar A∩B)=0.38
The probability that a defective component will be detected by exactly one of the two inspectors is 0.38
Part (C) All three defective components in a batch escape detection by both inspectors
This can be written as: P(bar A∪ bar B)-P(bar A∩B)-P(A∩ barB)
As we know bar P(A∩B)=P(bar A∪ bar B)=0.38
From part (B): P(bar A∩B)+P(A∩bar B)=0.38
This can be written as:
P(bar A∪ bar B)-P(bar A∩B)-P(A∩bar B)=0.38-0.38=0
The probability that all three defective components in a batch escape detection by both inspectors is 0
To know more about the probability:
https://brainly.com/question/13485191
#SPJ4