Answers
Answer:
LOL
Step-by-step explanation:
Answer:
for real they need to go
Step-by-step explanation:
Related Questions
If a one-way between-subjects ANOVA involved 48 people, and one independent variable with 5 levels/conditions, what would be the critical value of F if using an alpha of .01?
CHOOSE ONE
A. 2.589
B. 3.737
C. 3.476
D. 3.790
Answers
To determine the critical value of F for a one-way between-subjects ANOVA with 5 levels and 48 people, we need to find the degrees of freedom for the numerator and the denominator.
The numerator degrees of freedom (df₁) is equal to the number of levels minus 1, which is 5 - 1 = 4.
The denominator degrees of freedom (df₂) is equal to the total number of people minus the number of levels, which is 48 - 5 = 43.
Using these degrees of freedom, we can look up the critical value of F from the F-distribution table or use statistical software.
For an alpha level of 0.01 and df₁ = 4 and df₂ = 43, the critical value of F is approximately 3.737.
Therefore, the correct answer is B. 3.737.
Learn more about ANOVA here -: brainly.com/question/14984889
#SPJ11
9.99 rounded to the nearest hundreth
Answers
Answer:
9.99
Step-by-step explanation:
You want 9.99 rounded to the nearest hundredth.
PrecisionThe number you are given is already expressed to the precision you want, so nothing need be done.
9.99 . . . . . the value you want
RoundingOrdinarily, the process of rounding numbers is used to reduce their precision. The digit to the right of the place being rounded to is examined. If it is 5 or more, then the digit in the place being rounded to is increased by 1. All digits to the right of the place being rounded to are dropped.
Example
9.995 rounds to 10.00 when rounded to the hundredths place.
9.994 rounds to 9.99 when rounded to the hundredths place.
Rearrange each of the following in slope/y-intercept form, y = mx + b.
a. 3x - 6y + 8 = 0 b. -2x - 5y - 2 = 0
Answers
Answer:
a.
\({ \tt{3x - 6y + 8 = 0}} \\ { \tt{ 6y = 3x - 8}} \\ { \boxed{ \bf{y = \frac{1}{2} x - \frac{4}{3} }}}\)
b.
\({ \tt{ - 2x - 5y - 2 = 0}} \\ { \tt{5y = - 2x + 2}} \\ { \boxed{ \bf{y = - \frac{ 2}{5} x + \frac{2}{5} }}}\)
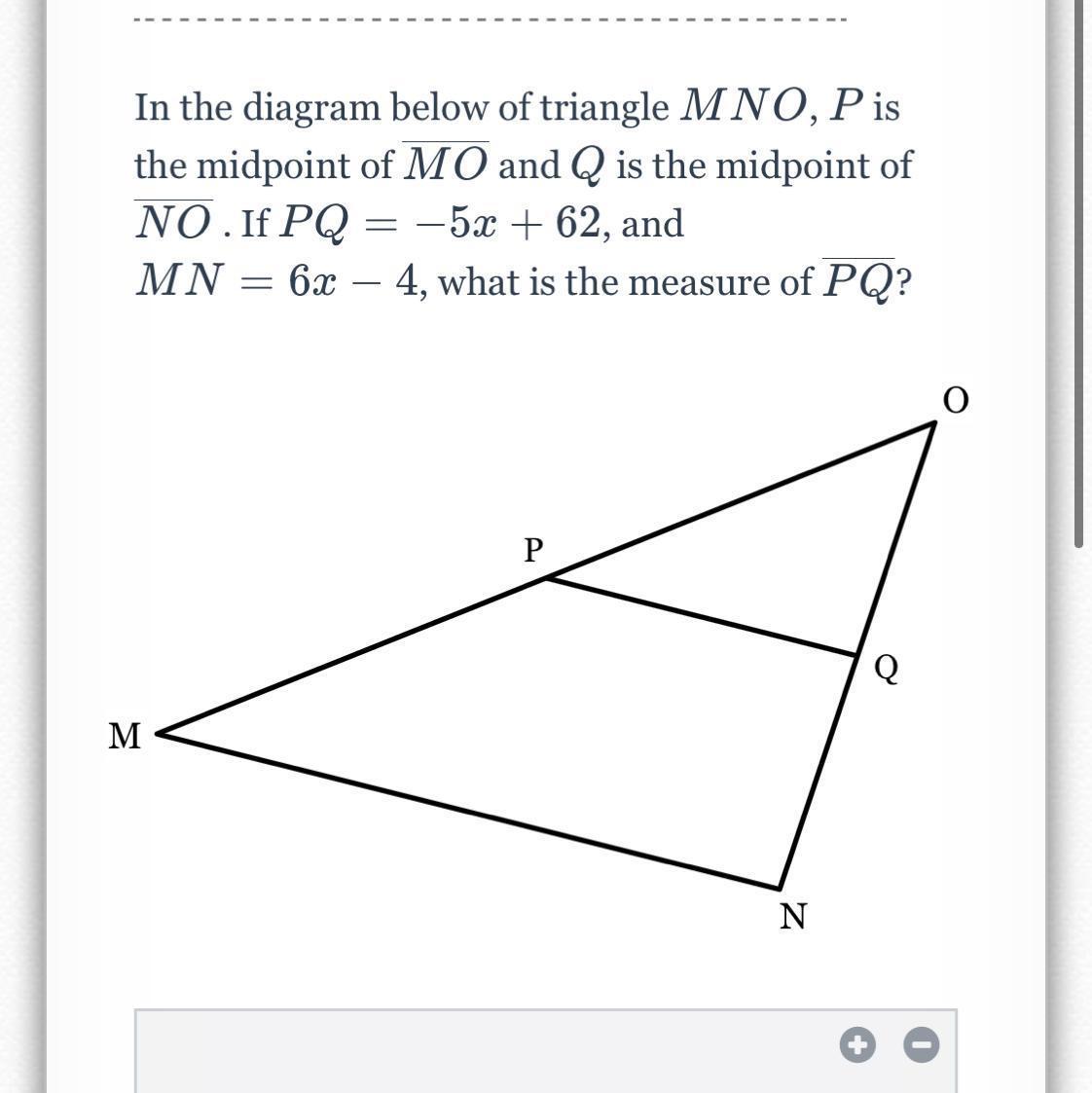
In the diagram below of triangle MNOP, P is the midpoint of MO and Q is the midpoint of NO. If PQ=5x+62 and MN=6x-4, what is the measure of PQ
Answers
The measure of length PQ will be 22 units.
What is the mid-point theorem?A triangle's third side is stated to be parallel to the line segment uniting its two midpoints, and it is also half as long as the third side.
Given:
PQ = 5x + 62, and MN = 6x-4
Now, using Mid- Point Theorem
PQ= 1/2 MN
-5x+ 62 = 1/2( 6x - 4)
-5x+ 62 = 3x - 2
-5x- 3x = -2 - 62
-8x = -64
x= 8
PQ= 5x+ 62 = -5(8) + 62 = -40 + 62 = 22
Hence, the measure of PQ is 22 units.
The missing image is attached below.
Learn more about the midpoint theorem here:
brainly.com/question/13677972
#SPJ1
NEED answer soon. just the 4 letters thankss

Answers
Answer:
a = 25m^2
b = 5m
d = 35.73 m^2
c = 7.94m
Step-by-step explanation:
First, remember that the area of a square of side length L is:
A = L^2
And for a triangle rectangle with catheti a and b, and hypotenuse H, we have the relation:
H^2 = a^2 + b^2 (Phytagorean's theorem)
Ok, let's look at the left image, we have a green triangle rectangle.
The bottom cathetus has a length equal to the side length of a square with area of 16m^2
Then the side length of that square (and the cathetus) is:
L^2 = 16m^2
L = √(16m^2) = 4m
The left cathetus has a length equal to the side length of a square of area = 9m^2
Then the side length of that cathetus is:
K^2 = 9m^2
K = √(9m^) = 3m
Then the catheti of the green triangle rectangle are:
4m and 3m
Then the hypotenuse of this triangle (b) is:
b^2 = (4m)^2 + (3m)^2
b^2 = 16m^2 + 9m^2 = 25m^2
b = √(25m^2) = 5m
And b is the side length of the red square, then the area of that square is:
a = b^2 = 25m^2
Now let's go to the other image.
Here we have an hypotenuse of side length H, such that:
H^2 = 144m^2
And we have a cathetus (the one adjacent to the green triangle) of side length L such that:
L^2 = 81m^2
The other cathetus will have a sidelength c, such that:
c^2 = area of the purple square
By the Pythagorean's theorem we have:
144m^2 = 81m^2 + c^2
144m^2 = 81m^2 + c^2
144m^2 - 81m^2 = c^2
63m^2 = c^2
(√63m^2) = c = 7.94m
And the area of a triangle rectangle is equal to the product between the catheti divided by two.
We know that one cathetus is equal to c = 7.94m
And the other on is equal to the square root of 81m^2
√(81m^2) = 9m
then the area of the triangle is:
d = (7.94m)*(9m)/2 = 35.73 m^2
Use the figure to find the radius.
4
4√2
4√3

Answers
The radius of the figure is 2√2.
We have,
From the figure,
The right angle triangle.
One angle is 90 and the other two angles will be the same. ie. 45
Now,
The sides opposite to the equal angles are the same.
From the figure,
Side = 2
Now,
Applying the Pythagorean theorem,
radius² = side² + side²
radius² = 2² + 2²
radius² = 4 + 4
radius = √8 = 2√2
Thus,
The radius of the figure is 2√2.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
jenelle draws one card from a standard deck of 52 cards. determine the probability of drawing either a queen or a king? write your answer as a reduced fraction. answer
Answers
Answer:
18/7
Step-by-step explanation:
check this might work as I simply
A box has the shape of a rectangular prism with height 33 cm. If the height is increased by 0.6 cm, by how much does the surface area of the box increase? Use pencil and paper. Show your work. Then show a second way to solve the problem. Explain which way you like better and why. 15 cm 6.3 cm The surface area increases by cm- 33cm. 6.3cm 15cm

Answers
The total increase in surface area is 189 cm², indicating that there has been a combined growth or expansion of surfaces by 189 square centimeters in the given context or scenario.
To find the increase in surface area of the box, we need to calculate the difference between the new surface area and the original surface area.
Let's calculate the original surface area:
Original surface area = 2(length × breadth + length × height + breadth × height)
= 2(15 cm × 6.3 cm + 15 cm × 33 cm + 6.3 cm × 33 cm)
= 2(94.5 cm² + 495 cm² + 207.9 cm²)
= 2(797.4 cm²)
= 1594.8 cm²
Now, let's calculate the new surface area when the height is increased by 0.6 cm:
New surface area = 2(15 cm × 6.3 cm + 15 cm × (33 cm + 0.6 cm) + 6.3 cm × (33 cm + 0.6 cm))
= 2(15 cm × 6.3 cm + 15 cm × 33.6 cm + 6.3 cm × 33.6 cm)
= 2(94.5 cm² + 501 cm² + 211.68 cm²)
= 2(807.18 cm²)
= 1614.36 cm²
Now, we can calculate the increase in surface area:
Increase in surface area = New surface area - Original surface area
= 1614.36 cm² - 1594.8 cm²
= 19.56 cm²
Second approach:
The increase in surface area can also be calculated by considering only the two faces affected by the change in height, which are the top and bottom faces of the box.
Each face has a length of 15 cm and a breadth of 6.3 cm. The increase in height is 0.6 cm.
The increase in surface area of one face = 15 cm × 6.3 cm
= 94.5 cm²
Since there are two faces (top and bottom), the total increase in surface area is:
Total increase in surface area = 2 × 94.5 cm²
= 189 cm²
For more such questions on surface area visit:
https://brainly.com/question/951562
#SPJ8
point b has coordinates (3,1). the x-coordinate of point a is -1. the distance between point a and point b is 5 units. what are the possible coordinates of point a?
Answers
The possible coordinates of point A are (-1, -2) and (-1, 4)
what are coordinates ?
Coordinates are sets of values that locate a point in a given space or plane. In mathematics, coordinates are commonly used to locate points on a graph, such as the Cartesian plane, which has two axes, the x-axis and y-axis, with perpendicular lines representing different values. The coordinates of a point are typically represented as an ordered pair, (x, y), where x represents the horizontal distance from the origin along the x-axis and y represents the vertical distance from the origin along the y-axis.
According to the question:
We know that the x-coordinate of point A is -1. Let's assume the y-coordinate of point A to be y.
Using the distance formula, we can find the distance between points A and B:
\(distance = \sqrt{((x2 - x1)^2 + (y2 - y1)^2)}\)
\(5 =\sqrt{((3 - (-1))^2 + (1 - y)^2)}\)
Simplifying the equation, we get:
\(25 = 16 + (1 - y)^2\)
\(9 = (1 - y)^2\)
\(\±3 = 1 - y\)
\(y = -2 or 4\)
Therefore, the possible coordinates of point A are (-1, -2) and (-1, 4).
To know more about coordinates visit:
https://brainly.com/question/29092536
#SPJ1
I forgot how to do this, I need an explanation to find the answer

Answers
Answer:
23.53
Step-by-step explanation:
OK so we got sin 52°=0.8 and the cos 52°=0.6
but we need tan 52° because we don't want to spend our time on calculating hypothenuse so
\( \frac{ \sin(52) }{ \cos(52) } = 1.3 = \tan(52) \)
so
\(1.3 = \frac{x}{18.1} = = = > x = 23.53\)
work out the total surface area of the pyramid

Answers
The total surface area of the pyramid is 335 square centimeters
How to determine the total surface areaThe formula for determining the total surface area of a pyramid is expressed as;
TSI = 1/2(PI) + B
Given that;
TSI is the total surface area of the pyramidP is the base perimeter of the pyramidI is the slant height of the pyramidB is the base area of the pyramidNow, let's determine the base perimeter
Perimeter = 2( l + w)
Substitute the values
Perimeter = 2 ( 8 + 12)
Perimeter = 40 centimeters
The base area is given as;
Base area = 8(12)
Base area = 96 square centimeters
Substitute the values, we have;
Total surface area = 1/ 2 (40)(12) + 96
Total surface area = 240 + 96
Total surface area = 335 square centimeters
Hence, the value is 335 square centimeters
Learn more about total surface area here:
https://brainly.com/question/26638955
#SPJ1
Is the point (5, –9) a solution in the equation y < -x -3
Answers
Answer:
yes, because if you input 5 for x it would be -8
and if u input -9 for y it is right as -8 is closer to 0 than -9
find the general solution of the differential equation1. dy/dx = 2x/y2. dy/dx = x(y+4)
Answers
The general solution for the second differential equation is y = \(e^[(1/2)x^2 + C2] - 4\)
1. \(dy/dx = 2x/y\)
Step 1: Separate variables. To do this, multiply both sides by y and divide both sides by dx:
\(y dy = 2x dx\)
Step 2: Integrate both sides:
\(∫y dy = ∫2x dx\)
Step 3: Evaluate the integrals:
\((1/2)y^2 = x^2 + C1\), where C1 is the constant of integration.
Step 4: Solve for y to obtain the general solution:
\(y^2 = 2x^2 + 2C1\\y = ±√(2x^2 + 2C1)\)
So, the general solution for the first differential equation is \(y = ±√(2x^2 + 2C1\)).
2. \(dy/dx = x(y+4)\)
Step 1: Separate variables. To do this, divide both sides by (y+4) and multiply both sides by dx:
\(dy / (y+4) = x dx\)
Step 2: Integrate both sides:
\(∫[1 / (y+4)] dy = ∫x dx\)
Step 3: Evaluate the integrals:
\(ln|y+4| = (1/2)x^2 + C2\), where C2 is the constant of integration.
Step 4: Solve for y to obtain the general solution:
\(y+4 = e^[(1/2)x^2 + C2]\\y = e^[(1/2)x^2 + C2] - 4\)
So, the general solution for the second differential equation is y = \(e^[(1/2)x^2 + C2] - 4\)
Learn more about differential here:
https://brainly.com/question/1603302
#SPJ11
The speed of a car from point A to D is m/s however the velocity is 10 m/s due West. Calculate the speed of vehicle in m/s if it covers a distance of 1.5 km in 5 minutes.
Answers
Speed of car is 5 m/sec
What is speed?
In ordinary language and kinematics, an object's speed is defined as the magnitude of its position change over time or the magnitude of its position change per unit of time; it is therefore a scalar number. The distance traveled by an item in a time interval is divided by the duration of the period; the instantaneous speed is the limitation of the average speed as the length of time period tends to zero. Velocity is not the same as speed. Distance divided by time is the dimension of speed. The metre per second (m/s) is the SI unit of speed, while the kilometre per hour (km/h) is the usual unit.
The speed of the car = 1.5/5 km/min = 0.3 km/min
Speed in m/sec = 0.3x1000/60 = 5m/sec
Hence, speed of car = 5 m/sec
To know more about speed, click on the link
https://brainly.com/question/13262646
#SPJ9
FILL IN THE BLANK. A good way to get a small standard error is to use a ________.1. Large sample2. Large population3. Repeated sampling4. Small sample5. Small population
Answers
A good way to get a small standard error is to use a Large sample. the correct answer is option 1.
The standard error is a measure of the variability of the sampling distribution of a statistic. A smaller standard error indicates that the statistic is more precise and is likely closer to the true population value.
One way to obtain a smaller standard error is to use a larger sample size. This is because a larger sample size tends to produce a more accurate estimate of the population parameter, with less variability. Therefore, option 1, "Large sample," is the correct answer.
The other options, such as a large population, repeated sampling, small sample, or small population, are not necessarily related to obtaining a small standard error.
To learn more about standard error click on,
https://brainly.com/question/13179711
#SPJ11
if you had 12.3 grams of carbohydrates, how many calories would that contribute per serving? do not round; give the absolute value.
Answers
49.2 calories are in would that contribute per serving .
What does a calorie mean ?
Energy is measured in calories. When you hear something has 100 calories, it means that it has the potential to provide your body with that many calories of energy. Calories are the units of energy used by your body during food digestion and absorption. A food's ability to give your body energy depends on how many calories it contains.Carbohydrates provide 4 calories per gram.
1 gm Carbohydrates = 4 calories
then 12.3 gm Carbohydrates = 12.3 * 4
= 49.2 calories
Learn more about calories
brainly.com/question/22374134
#SPJ4
(41/3-12/4) divided 4/15
Answers
Answer: 40
\(\frac{41}{3} -\frac{12}{4} =\frac{41(4)-12(3)}{12} =\frac{164-36}{12} =\frac{128}{12} =\frac{32}{3}\\\\\frac{\frac{32}{3}}{\frac{4}{15} } =\frac{32}{3}*\frac{15}{4} =\frac{8(4)}{3}*\frac{5(3)}{4}=40\)
which histogram most likely represents a country with a declining population growth rate?
Answers
The histogram that most likely represents a country with a declining population growth rate is one where the bars to the right (representing higher numbers of births or deaths) are lower than the bars to the left.
A declining population growth rate means that the rate at which the population is growing is decreasing, which suggests that the number of births is decreasing or the number of deaths is increasing.
In other words, the shape of the histogram would be skewed to the left, with a long tail on the left-hand side and shorter bars on the right-hand side. This shape suggests that there are fewer births or more deaths, leading to a declining population growth rate.
It is worth noting that a histogram alone may not provide enough information to make definitive conclusions about population growth rates. Other factors such as migration rates and changes in life expectancy can also affect population growth. Therefore, it is important to consider multiple sources of data and statistical methods when analyzing population trends.
To learn more about histograms
https://brainly.com/question/30664111
#SPJ4
write an equation of a line passing through point p(-2, 6) that is parallel to the line x= -5
Answers
Answer:
x= -2
Step-by-step explanation:
x = -5 is a vertical line, so a line parallel would also have to be a vertical line
It goes through the point ( -2,6)
The x coordinate -2
So a line parallel would be x= -2
Answer:
x= -2
Step-by-step explanation:
If log3 x + logx 3= 2.5 find the value of x
Answers
The value of x is -0.004624
\(log_{3} (x)+log_{x} (3)=2.5\)
\(log_{3} (x)+\frac{log_{3} (3)}{log_{3} (x)} =2.5\)
Let z= \(log_{3} (x)\)
\(z+\frac{1}{z} = 2.5\)
\(3z^{2} + z-2.5z=0\)
z= -0.166
\(log_{3} (x)=-0.166\)
x = -0.004624
What is a log?
The logarithm is exponentiation's opposite function in mathematics. This indicates that the exponent to which a set number, base b, must be increased in order to create a specific number x, is represented by the logarithm of that number. The logarithm, in its most basic form, counts the number of times the same factor appears when multiplied repeatedly; for instance, since 1000 = 10 x 10 x 10 = 103, its "logarithm base 10" is 3, or log10 (1000) = 3. When there is no possibility of a mistake or when the base is irrelevant, as, in big O notation, the logarithm of x to base b is written as loga (x), logb x, or even without the explicit base, log x.
Learn more about logarithm https://brainly.com/question/28346542
#SPJ1
A differentiable function y(x), and x > 0, that satisfies the IVP y’ |x|, y(-1)= 2 is
Answers
To find a differentiable function y(x) that satisfies the initial value problem (IVP) y' = |x| and y(-1) = 2, we can integrate the given differential equation and then apply the initial condition.
Integrating both sides of the differential equation y' = |x| with respect to x, we get:
∫ y' dx = ∫ |x| dx
Integrating ∫ y' dx gives us y(x) + C₁, where C₁ is an arbitrary constant of integration.
Integrating ∫ |x| dx involves considering the different cases for x. Since x > 0 (as given in the problem), we have:
∫ |x| dx = ∫ x dx (for x > 0)
= (x^2)/2 + C₂, where C₂ is another arbitrary constant of integration.
Now, we have:
y(x) + C₁ = (x^2)/2 + C₂
To determine the values of C₁ and C₂, we can use the initial condition y(-1) = 2:
y(-1) + C₁ = ((-1)^2)/2 + C₂
2 + C₁ = 1/2 + C₂
Simplifying further:
C₁ = 1/2 - 2 + C₂
C₁ = C₂ - 3/2
We can rewrite the equation for y(x) by substituting C₁ with C₂ - 3/2:
y(x) = (x^2)/2 + (C₂ - 3/2)
Therefore, a differentiable function that satisfies the given IVP y' = |x| and y(-1) = 2 is:
y(x) = (x^2)/2 + (C₂ - 3/2), where C₂ is an arbitrary constant.
Learn more about differentiable function here:
https://brainly.com/question/18962394
#SPJ11
hi can someone pls pls plsss! Help with this, I have a test and it’s due on Tuesday so I have time but for now can you pls help because this is apart of the test/practice so it’d be rlly helpful thanks!<333 have a good day!

Answers
Answer:
16 square feet is left uncovered.
Explanation:
Essentially, you’re trying to find the difference between the area of the door and the area of the poster. The area formula for a basic rectangle is l • w (length times width.) We have both of those dimensions for the separate shapes, so you can go ahead & do that math separately (as shown in the attachment!) Then, you subtract the area of the poster from the area of the door, and you have your answer. As always, I hope this is accurate & helpful! Good luck on your test, friend. Best wishes <3

Write a cubic function for the graph shown here:
Explain and show work.

Answers
The cubic equation graphed is
f(x) = (x + 4) (x + 2) (x + 2)How to find the cubic equationWe find the cubic equation by taking note of the roots. The roots are the x-intercepts and investigation of the graph shows that the roots are
(x + 4), (x + 2), and (x + 2)
We can solve for the equation as follows
f(x) = a(x + 4) (x + 2) (x + 2)
Using point (0, 16)
16 = a(0 + 4) (0 + 2) (0 + 2)
16 = a * 4 * 2 * 2
16 = 16a
a = 1
Therefore, the equation is f(x) = (x + 4) (x + 2) (x + 2)
Learn more about cubic equation at
https://brainly.com/question/1266417
#SPJ1
A tree was 8 feet tall when it was planted. After 5 years, it was 18 feet tall. What was the tree's growth rate?
O a
8 feet per year.
b
3.6 feet per year.
2 feet per year.
1.6 feet per year.
Oc
Od
Answers
Answer:
2
Step-by-step explanation:
It grew (18-8) = 10 feet in 5 years
10 ft / 5 yr = 2ft/yr
The perimeter of this figure is 70 feet. How long are the unknown sides?
A) 12ft
B)6ft
C)5ft
D)10ft
I should know this but I don’t and I need help or just an answer 50 points

Answers
The length of the unknown sides as described in the task content is; Choice B; 6 ft.
What is the length of the unknown sides?Since the perimeter of a figure is the sum of all of its side lengths;
Therefore;
Perimeter = 14 + 10 + 12 + 10 + 5 + 7 + x + x
70 = 58 + 2x
2x = 12
x = 6ft.
Ultimately, the length of the unknown sides x is; 6.
Read more on perimeter of a figure;
https://brainly.com/question/24474373
#SPJ1
How many vectors (x1, x2, ..., xk) are there for which each xi is apositive integer such that 1 ≤ xi ≤ n and x1 < x2< · · · < xk?
Sln: For each of such vectors we just have a set of k differentnumbers
chosen from 1 to n, and for each set of k different numbers chosenfrom
1 to n we can get one and only one vector like in the statement ofthe
problem, since there’s only one way to order the chosennumbers in
increasing order. Thus the number of required vectors is the sameas
the numbers of sets with k elements taken from a set of nelements,
(n
k)
How many vectors (x1, x2, ..., xk) are there
for which each xi is a positive integer such that 1 ≤ xi≤ n and
x1 ≤ x2 ≤ · · · ≤ xk?
I have an idea to what this answer is but not sure. Any helpwill be appreciated.
Thanks
Answers
The number of vectors (x1, x2, ..., xk) where each xi is a positive integer such that 1 ≤ xi ≤ n and x1 ≤ x2 ≤ · · · ≤ xk is (n+k-2) choose (k-1).
For the second problem, we want to find the number of vectors (x1, x2, ..., xk) where each xi is a positive integer such that 1 ≤ xi ≤ n and x1 ≤ x2 ≤ · · · ≤ xk.
We can approach this problem using the stars and bars method. Imagine we have k stars, and we want to divide them into k groups, with each group representing the value of one of the xi. We can use k-1 bars to separate the stars into k groups. For example, if k=4, n=5, and the vector is (1,1,4,4), we can represent this as:
| * * | | *
The first two stars represent x1, the next two stars represent x2, the next zero stars represent x3, and the last star represents x4.
Since each xi must be at least 1, we can place one star in each group before placing the remaining k-n stars. Then we have k-n remaining stars to distribute among the k groups. This can be done using the stars and bars formula, which gives us:
(n-1+k-n) choose (k-1) = (n+k-2) choose (k-1)
For example, if n=5 and k=3, the number of vectors is (5+3-2) choose (3-1) = 6 choose 2 = 15.
For more similar questions on vectors:
https://brainly.com/question/29708786
#SPJ11
3 gallons But in pints
Answers
Answer: 24 pints
Step-by-step explanation:
multiply the volume value by 8
3*8=24
The rental price of a dacha was $9000. At the end of each month
the price is increased by 6%.
a) Find the price of the house after 1 month.
b) Find the price of the house after 3 months.
c) Find the price of the house after 10 months
Answers
a) The price (amount) of the house after 1 month = $9540
b) The price (amount) of the house after 3 months = $10719.14
c) The price (amount) of the house after 10 months = $16117.629
a ) How to find the rental price of the house after 1 month ?
The rental price of a dacha = Principle = $9000
Percentage increase in price = r = 6%
Number of months = n = 1
Amount of a compound interest is given by,
\(Amount = P(1 +\frac{r}{100} )^n\\\\=9000( 1 +\frac{6}{100}) \\\\= 9000(\frac{106}{100})\\\\= 90*106\\\\= 9540\)
The rental price of the house after 1 month = $9540
b ) How to find the rental price of the house after 3 months ?
The rental price of a dacha = Principle = $9000
Percentage increase in price = r = 6%
Number of months = n = 3
Amount of a compound interest is given by,
\(Amount = P(1 +\frac{r}{100} )^n\\\\=9000( 1 +\frac{6}{100})^3 \\\\= 9000(\frac{106}{100})^3\\\\= 9000*(1.06)^3\\\\= 10719.14\)
The rental price of the house after 3 months = $10719.14
c ) How to find the rental price of the house after 10 months ?
The rental price of a dacha =Principle = $9000
Percentage increase in price = r = 6%
Number of months = n = 10
Amount of a compound interest is given by,
\(Amount = P(1 +\frac{r}{100} )^n\\\\=9000( 1 +\frac{6}{100})^{10} \\\\= 9000(\frac{106}{100})^{10}\\\\= 9000*(1.06)^{10}\\\\= 9000*1.790\\\\= 16117.629\)
The rental price of the house after 10 months = $16117.629
To learn more about compound interest, refer:
https://brainly.com/question/24924853
#SPJ4
Sammy went to visit his grandma. He traveled by bus for 24% of his trip. How long was Sammy's trip if he traveled 15 miles by bus?
Answers
PLEASE HELP!! find the slope of the graph asap!

Answers
Answer: I do not understand
Step-by-step explanation:
