Answers
Answer:
y =
\( \frac{256}{3} \)
× =
\( \frac{8192}{75} \)
I HOPE IT CAN HELP:)
Step-by-step explanation:
you first multiply 5 by y and 25 by 6.4 you will get y as 32 and you fix it into the first equation and get x
Related Questions
If the area of an equilateral triangle is 49 root 3 centimeter square. Find the perimeter.
Answers
Answer:
14 ×3 = 42 cm.
Step-by-step explanation:
Can someone help me super fast? The answers are (m+5n) (m-n) and (a+4b) (a-3b) I just need to know how to get them cuz my calculations aren't working

Answers
Let's see
#1
(m+5n)(m-n)m(m-n)+5n(m-n)m²-mn+5nm-5n²m²+4n-5n²#2
(a+4b)(a-3b)a(a-3b)+4b(a-3b)a²-3ab+4ab-12b²a²+ab-12b²
Without using logarithm tables, find the value of x given that: 2log2/3 = 1/2logx - log 18 + log 16
Answers
Answer:
\(x=\frac{1}{4}\)
Step-by-step explanation:
Given:
\(2log(\frac{2}{3})=\frac{1}{2}log(x)-log(18)+log(16)\)
Use the Power Rule Law:
\(log(\frac{2}{3}^2)=log(x^{1/2})+log(16)-log(18)\)
Use the Quotient Rule Law:
\(log(\frac{4}{9})=log(\sqrt{x})+log(\frac{16}{18})\)
Use the Product Rule Law:
\(log(\frac{4}{9})=log(\frac{16\sqrt{x}}{18})\)
Simplify:
\(log(\frac{4}{9})=log(\frac{8\sqrt{x}}{9})\)
\(\frac{4}{9}=\frac{8\sqrt{x}}{9}\)
\(4=8\sqrt{x}\)
\(\frac{4}{8}=\sqrt{x}\)
\(\frac{1}{2}=\sqrt{x}\)
\(\frac{1}{4}=x\)
What would be the first step in the following expression? :4+6×8–3+4
Answers
Answer:
Working the multiplication part ( that is; 6×8)
Step-by-step explanation:
There is a path of width 2.5 m inside around a square garden of length 45m.
(a) Find the area of the path.
(b) How many tiles will be required to pave in the path by the square tiles of length 0.5m? Find it.
Help ! 도와주세요, 제발 :(
Answers
Answer:
2.5+2.5+45+45
=95.0m
therefore area of the square= 95.0m
45m×0.5=45.5÷95=
Step-by-step explanation:
2.5m
2.5 m tiles are required
\(area = 2.5 \times 45 = 192.5 \: squared \: cenimetre \\ \\ no \: of \: tiles = 0.5 \times 0.5 = 0.25 \\ 192.5 \div 0.25 = 770tiles\)
pls help this is the last question and i have to get correct

Answers
The correct statements regarding sum and subtraction with negative numbers are given as follows:
The inequality p + q < 0 is possible because -5 + (-5) = -10.The inequality p - q > 0 is possible because -4 - (-5) = 1.The inequality p - q < 0 is possible because -5 - (-4) = -1.How to add two negative numbers?When two negative numbers are added, the result is negative, as we keep the signal and then add the absolute amounts of each value, for example:
-5 + (-5) = -(5 + 5) = -10.
Hence the fourth statement is correct, while the first and the third are not.
How to subtract two negative numbers?When we subtract two negative numbers, we first transform the second number to positive, meaning that the result can be either positive or negative, as the result will take the signal of the higher value and their absolute amounts are subtracted.
Hence:
-4 - (-5) = -4 + 5 = (5 - 4) = 1.-5 - (-4) = -5 + 4 = -(5 - 4) = -1.Hence the fifth and the sixth statements are correct.
More can be learned about sum and subtraction with negative numbers at https://brainly.com/question/572656
#SPJ1
What is the value of the expression shown? 7 x [(7 + 7) ÷ 7]
Answers
Answer:
14
Step-by-step explanation:
Follow BPEMDAS, or PBEMDAS in this case:
PBEMDAS stands for:
Parenthesis
Brackets
Exponents (& Roots)
Multiplication
Division
Addition
Subtraction
~
First, solve the parenthesis:
(7 + 7) = 14
Next, divide:
[14/7] = 2
Finally, multiply:
7 x 2 = 14
14 is your answer.
~
Pls help!
Whoever answers in a few minutes with a clear answer will be marked brainiest!!!
Use exponent laws to write each expression with a positive power

Answers
Answer:
a. \(\tt \frac{1}{9}\)
b. \(\frac{1}{16}\)
c. 4
Step-by-step explanation:
\(\tt a. \:3^{-2}\)
We can use the negative exponent rule, which states that \(\boxed{\tt a^{-n} = \frac{1}{a^n}}\) So, we have:
\(\tt 3^{-2} = \frac{1}{3^2} = \frac{1}{9}\)
\(\hrulefill\)
\(\tt b.\: -2^{-4}\)
We can use the rule that \(\boxed{\tt -a^{-n} = (-1)^n \cdot a^n}.\) So, we have:
\(\tt -2^{-4} = (-1)^4 \cdot 2^{-4} = 1 \cdot \frac{1}{2^4} = \frac{1}{16}\)
\(\hrulefill\)
\(\tt c. \:(\frac{1}{2})^{-2}\)
We can use the negative exponent rule, which states that \(\boxed{\tt a^{-n} = \frac{1}{a^n}}\). So, we have:
\(\tt (\frac{1}{2})^{-2} = \frac{1}{(\frac{1}{2})^2} = \frac{1}{\frac{1}{4}} = 4\)
Answer:
Step-by-step explanation:
(a) 3^-2 = 1/9
(b) (-2)^-4 = 1/(-2)^4 = 1/16
(c) (1/2)^-2 = 1/(1/2)^2=1 / 1/4 = 4
Rewrite the equation in Slope-Intercept Form. y+4=−12(x−2)
Answers
Answer: y = -12x +20
Step-by-step explanation: 1. distribute the -12 into the (x-2), that equals -12+24
2. subtract the 4 from the left side to move it to the right side of the equation
3. add like terms, so 24 + (-4) or 24-4 which equals 20.
4. Answer: y=-12x+20
11 less than the quotient of
4
44 and
�
xx.
Answers
The expression which is used to represents the statement "one-more than the quotient of a number x" and 4 is "x/4 + 1".
A "Quotient" is the result of a division operation between two numbers, where one number is divided by another. It represents the number of times one number is contained within another number.
An "Expression" is defined as "mathematical-phrase" which contain numbers, variables, and operators such as addition, subtraction, multiplication, and division. It can also contain functions and other mathematical symbols.
The quotient of a number"x" and 4 can be written as x/4.
So, one more than the quotient of a number x and 4 can be represented by the expression:
⇒ x/4 + 1,
Therefore, required mathematical expression is "x/4 + 1".
Learn more about Expression here
https://brainly.com/question/30553495
#SPJ1
The given question is incomplete, the complete question is
Write an expression to represent : One more than the quotient of a number x and 4.
Solve the triangle. Round to the nearest tenth.
Find c aswell

Answers
Answer:
Set your calculator to Degree mode.
a² = 17² + 20² - 2(20)(17)cos(89°)
a² = 677.13236
a = 26.0 in.
sin(89°)/26.02177 = (sin B)/17
sin B = 17sin(89°)/26.02177
B = 40.8°
C = 50.2°
A triangle has side lengths of 6, 8, and 10. Is it a right triangle? Explain.
Answers
Answer:
yes
Step-by-step explanation:
Yes it is, assuming we decide to use the Pythagorean Theorem to find the hypotenuse (10) it'll be possible considering the formula is c²=√a²+b²
(c being the longest side of the triangle)
a= 6 and b= 8
Need help on this question

Answers
PLS HELP I DONT UNDERSTAND!! :( WILL MARK BRAINLIEST!!

Answers
Answer:
8)b. 9)d.
Step-by-step explanation:
a biome is a type of group of plants and animals that belong in the same area. This is affected by how much rain a place gets, the temperatures of the place, and many other factors.
the atlantic ocean, russia, chile, central america, and alaska are not continents
Answer:
Question 8: B
Question 9: D
Step-by-step explanation:
8- The three examples explain 3 different climates and how the biomes affect the region.
9- The Continents are Asia, Africa, Europe, Antarctica, North America, South America, and Australia
Determine the equation of the circle with radius 9 and center ( − 1 , − 8 ).
Answers
The equation of the circle with radius 9 and center ( -1,-8 ) is( x + 1 )² + ( y + 8 )² = 81.
What is the equation of the circle?The standard form equation of a circle with center (h, k) and radius r is:
( x - h )² + ( y - k )² = r²
Given that the circle has a center of (-1, -8) and the radius is 9.
Hence; from the standard form of the equation of the circle:
Center ( h , k ) = ( -1, -8 )
h = -1
k = -8
And radius r = 9
Plug these values into the above formula and simplify.
( x - h )² + ( y - k )² = r²
( x - ( -1 ) )² + ( y - ( -8 ) )² = 9²
Simplify
( x + 1 )² + ( y + 8 )² = 81
Therefore, the equation of the circle is ( x + 1 )² + ( y + 8 )² = 81.
Learn more about equation of circle here: brainly.com/question/29288238
#SPJ1
Anyones let me know how to do it?

Answers
Answer:
B
Step-by-step explanation:
assuming you require problem 3
using the Sine Rule in Δ ABC and the exact values
sin45° = \(\frac{1}{\sqrt{2} }\) , sin30° = \(\frac{1}{2}\)
\(\frac{AB}{sin45}\) = \(\frac{BC}{sin30}\) , that is
\(\frac{8}{sin45}\) = \(\frac{BC}{sin30}\) ( cross- multiply )
BC sin45° = 8 sin30°
BC × \(\frac{1}{\sqrt{2} }\) = 8 × \(\frac{1}{2}\) = 4 ( multiply both sides by \(\sqrt{2}\) to clear the fraction )
BC = 4\(\sqrt{2}\)
If x + 1/x = 83, find the value of x^2 + 1/x^2
Answers
Answer:
6887
Step-by-step explanation:
given
x + \(\frac{1}{x}\) = 83 ( square both sides )
(x + \(\frac{1}{x}\) )² = 83² = 6889 ← expand factor on left using FOIL
x² + 2( x × \(\frac{1}{x}\) ) + \(\frac{1}{x^2}\) = 6889
x² + 2(1) + \(\frac{1}{x^2}\) = 6889 ( subtract 2 from both sides )
x² + \(\frac{1}{x^2}\) = 6887
Half of a substance will decay after 10 hours. If 150 g of a substance is present inititially, how much would be left after 3 days?
Answers
Ayuda operaciones y respuesta es para ahora

Answers
The perimeter of the given window is 48 centimeter.
From the given figure,
Perimeter of window = 2(Length+Breadth)
= 2(10+14)
= 2×24
= 48 centimeter
Perimeter of house = 2(Length+Breadth)
= 2(37+35)
= 2×72
= 144 centimeter
Perimeter of roof = 2(Length+Breadth)
= 2(37+5)
= 2×42
= 84 centimeter
Therefore, the perimeter of the given window is 48 centimeter.
To learn more about the perimeter visit:
https://brainly.com/question/6465134.
#SPJ1
The assistant manager of a surf shop estimates that 65% of customers will make a purchase
Part A: How many customers should a salesperson expect until he finds a customer that makes a purchase?
Part B: What is the probability that a salesperson helps 3 customers until he finds the first person to make a purchase?
Answers
Using the binomial distribution, it is found that:
A. The salesperson should expect 1.54 customers until he finds one that makes a purchase.
B. There is a 0.0279 = 2.79% probability that a salesperson helps 3 customers until he finds the first person to make a purchase.
What is the binomial distribution formula?The formula is:
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes.n is the number of trials.p is the probability of a success on a single trial.For this problem, the probability of a success on a single trial is of p = 0.65.
The expected number of trials until q successes is:
E(X) = q/p
Hence, for one purchase:
E(X) = 1/0.65 = 1.54.
The salesperson should expect 1.54 customers until he finds one that makes a purchase.
For item B, the probability is P(X = 0) when n = 3 multiplied by 0.65, hence:
p = (0.35)³ x 0.65 = 0.0279.
There is a 0.0279 = 2.79% probability that a salesperson helps 3 customers until he finds the first person to make a purchase.
More can be learned about the binomial distribution at https://brainly.com/question/24863377
#SPJ1
Use the pair of functions to find f(g(x)) and g(f(x)). Simplify your answers.
f(x)= 1= ² + 4
X-4

Answers
To find f(g(x)), we need to substitute g(x) into the function f(x). Given that g(x) = x - 4, we substitute it into f(x) as follows:
\(f(g(x)) = f(x - 4) = (x - 4)^2 + 4\)
To simplify this expression, we can expand the square:
\(f(g(x)) = (x - 4)(x - 4) + 4\\ = x^2 - 8x + 16 + 4\\ = x^2 - 8x + 20\)
Therefore, f(g(x)) simplifies to\(x^2 - 8x + 20.\)
Next, let's find g(f(x)). We substitute f(x) into the function g(x):
\(g(f(x)) = g(1/x^2 + 4) = 1/x^2 + 4 - 4\\ = 1/x^2\)
Hence, g(f(x)) simplifies to 1/x^2.
In summary, f(g(x)) simplifies to\(x^2 - 8x + 20\), and g(f(x)) simplifies to 1/x^2.
For more such questions on functions
https://brainly.com/question/10439235
#SPJ8
compare1/2 with 3/4 using (<>=)
Answers
Answer: 3/4 is greater than 1/2
>
Step-by-step explanation:
Using digits 1to 9 fill in the boxes once write largest and smallest absolute value. Then find the decimal equivalent.
Answers
The decimal equivalent of the largest Absolute value, 987654321, is 987,654,321. the largest absolute value is 987,654,321 and the smallest absolute value is 123,456,789.
The largest and smallest absolute values using the digits 1 to 9, we need to arrange them in a way that maximizes or minimizes the resulting number. Let's consider the boxes as placeholders for the digits.
To determine the largest absolute value:
We place the digit 9 in the leftmost box, as it is the largest digit among 1 to 9. Then we arrange the remaining digits, 8, 7, 6, 5, 4, 3, 2, and 1, from largest to smallest in the remaining boxes. This gives us the number 987654321, which is the largest possible number using the given digits. Therefore, the largest absolute value is 987654321.
To determine the smallest absolute value:
We place the digit 1 in the leftmost box, as it is the smallest digit among 1 to 9. Then we arrange the remaining digits, 2, 3, 4, 5, 6, 7, 8, and 9, from smallest to largest in the remaining boxes. This gives us the number 123456789, which is the smallest possible number using the given digits. Therefore, the smallest absolute value is 123456789.
To find the decimal equivalent of these numbers, we simply read the digits from left to right. The decimal equivalent of the largest absolute value, 987654321, is 987,654,321. The decimal equivalent of the smallest absolute value, 123456789, is 123,456,789.
Thus, the largest absolute value is 987,654,321 and the smallest absolute value is 123,456,789.
To know more about Absolute value.
https://brainly.com/question/24368848
#SPJ8
For a confidence level of 98% with a sample size of 32, find the critical t value.
Answers
The critical value for a confidence level of 98% with a sample size of 32 is given as follows:
t = 2.4528.
What is a t-distribution confidence interval?The t-distribution is used when the standard deviation for the population is not known, and the bounds of the confidence interval are given according to the equation presented as follows:
\(\overline{x} \pm t\frac{s}{\sqrt{n}}\)
The variables of the equation are listed as follows:
\(\overline{x}\) is the sample mean.t is the critical value.n is the sample size.s is the standard deviation for the sample.The critical value, using a t-distribution calculator, for a two-tailed 98% confidence interval, with 32 - 1 = 31 df, is t = 2.4528.
(df is one less than the sample size).
More can be learned about the t-distribution at https://brainly.com/question/27701525
#SPJ1
The box and whisker plot shows the scores in the science test of two classes based on the distribution of data which observation is not correct

Answers
Based on the distribution of data, the box and whisker plot displays the results of the scientific test for two classes. It is incorrect to say that both sections have the same value for the third quartile.
The formulation of partial differential equation solutions uses distribution generalized functions. The likelihood of a specific value or range of values for a variable is known as the probability distribution. Cumulative distribution function, where the likelihood of a value not exceeding a certain value depends on that value. A list of the values recorded in a sample, or a frequency distribution. In coding theory, there are two types of distribution: inner and outer. distribution of a portion of a manifold's tangent bundle.Term distribution: the state of having all members of a category present. The distributive law from elementary algebra is generalized by the property of binary operations known as distributivity. the distribution.
Learn more about distribution from
https://brainly.com/question/23286309
#SPJ1
Find the measure of angle A.
60x
O 60°
O 30°
O 23°
O 37°
30x
A

Answers
Answer:
Step-by-step explanation:
sum of angles in a triangle=180º
90+60x+30x=180
90+90x=180
90(1+x)=180
1+x=2
x=1
angle A=30º
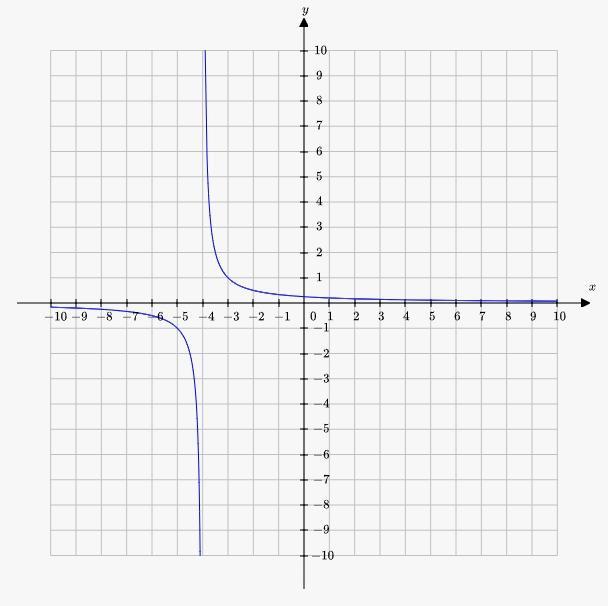
ANSWER THE FOLLOWING:

Answers
According to the given function,
Domain = \(\left(-\infty, -4\right) \cup \left(-4, 2\right) \cup \left(2, \infty\right)\)
Vertical Asymptote = 4
Horizontal Asymptote = 0
X - intercept = No x - intercepts
Y - intercept = 1/4
Domain:
The the domain of a function referred as the set of inputs accepted by the function
Given,
The function is,
\(f(x)=\frac{x-2}{x^2+2x-8}\)
Here we need to find the domain, vertical asymptote, horizontal asymptote, x - intercept, and y-intercept.
To find the domain and intercepts, we have to plot the graph for the given function.
So, the graph of the function is attached below. It can be drawn using the graphing calculator.
As per the graph,
Domain = \(\left(-\infty, -4\right) \cup \left(-4, 2\right) \cup \left(2, \infty\right)\)
And the values of
x - intercept = No x-intercepts
y - intercept = 1/4
Now, the vertical asymptote is calculated as,
The line x=L is a vertical asymptote of the function f(x), if the limit of the function (one-sided) at this point is infinite.
In other words, it means that possible points are points where the denominator equals 0 or doesn't exist.
So, find the points where the denominator equals 0 and check them.
x = -4
Then,
\(\lim_{x \to -4^+} \frac{1}{x + 4}=\infty\)
Since the limit is infinite, then x=−4 is a vertical asymptote.
And the horizontal asymptote is,
Line y=L is a horizontal asymptote of the function y=f(x), if either '
\(\lim_{x \to \infty} f{\left(x \right)}=L\) or \(\lim_{x \to -\infty} f{\left(x \right)}=L\) and L is finite.
When we calculate the limits:
\(\lim_{x \to \infty}\left(\frac{x - 2}{x^{2} + 2 x - 8}\right)=0\\\\\lim_{x \to -\infty}\left(\frac{x - 2}{x^{2} + 2 x - 8}\right)=0\)
Thus, the horizontal asymptote is y=0.
To know more about Domain here.
https://brainly.com/question/28135761
#SPJ1
Please awnser asap I will brainlist
Answers
The members of the given set in this problem are given as follows:
X U (Y ∩ Z) = {p, q, r, 0, 6, 21, 22, 23, 26}
How to obtain the union and intersection set of two sets?The union and intersection sets of multiple sets are defined as follows:
The union set is composed by the elements that belong to at least one of the sets.The intersection set is composed by the elements that belong to at all the sets.The intersection of the sets Y and Z for this problem is given as follows:
Y ∩ Z = {0, 6, 23, 26}
(which are the elements that belong to both of the sets).
The union of the above set with the set X is given as follows:
X U (Y ∩ Z) = {p, q, r, 0, 6, 21, 22, 23, 26}
(elements that belong to at least one of the sets).
More can be learned about union and intersection at brainly.com/question/4699996
#SPJ1
PLS HELP ME ANSWER THIS QUESTION..

Answers
Answer:
b. 4
c. 90⁰
Step-by-step explanation:
a. is in the diagram

$16.20 per hour for 40 hours and time and a half for 8 hours. What is the total pay?
Answers
Answer:
Add 16.20+ 40+8
Step-by-step explanation: 16+20+40+8= 84
