Answers
The quadratic equation that represents the stopping distance is stopping distance = 0.31x² - 18.38x + 402.8. The stopping distance for x = 50 is 258.8 units.
What is quadratic equation?The largest power of the variable in a quadratic equation, which is a polynomial equation of degree 2, is 2. A quadratic equation has the following general form:
ax² + bx + c
where a 0 and the constants a, b, and c are present together with the variable x. The quadratic term is designated as ax2; the linear term is bx; and the constant term is c.
Using the given data points for the truck we have:
169 = a(40)² + b(40) + c
169 = 1600a + 40b + c (equation 1)
335 = a(55)² + b(55) + c
335 = 3025a + 55b + c (equation 2)
525 = a(65)² + b(65) + c
525 = 4225a + 65b + c (equation 3)
Subtracting the equation 1 and 2 we have:
335 = 3025a + 55b + c
- 169 = -1600a - 40b - c
166 = 1425a + 15b (equation 4)
Subtract equation 2 from 3:
525 = 4225a + 65b + c
- (335 = 3025a + 55b + c)
190 = 1200a + 10b (equation 5)
Equation 5 can be written as:
190 - 1200a = 10 b
b = 19 - 120a
Substituting the value of b in equation 4 we have:
166 = 1425a + 15(19 - 120a)
166 = 1425a + 285 - 1800a
166 - 285 = -375a
-119 = -375a
a = 0.31
Now, substitute the value of a in equation 4:
166 = 1425a + 15b
166 = 1425(0.31) + 15b
b = -18.38
Now, substitute the value of a and b in equation 1:
169 = 1600a + 40b + c
169 = 1600(0.31) + 40(-18.38) + c
c = 402.8
Hence, the quadratic equation that represents the stopping distance is:
stopping distance = 0.31x² - 18.38x + 402.8
Now, for x = 50 we have:
stopping distance = 0.31(50)² - 18.38(50) + 402.8 = 258.8
Hence, the stopping distance for x = 50 is 258.8 units.
Learn more about quadratic equation here:
https://brainly.com/question/30098550
#SPJ1
Related Questions
To celebrate the holiday season this year, the Gaylord Texan has created an extreme eight-lane, tubing hill
with real snow called the "Kung Fu Panda Awesome SNOW Tubing Ride." The cost of each ticket for one day
is $21. This can be modeled by the function f(x) = 21x. The number of tickets purchased by groups is given
by the domain (4, 6, 103. which would be a reasonable range for the total cost of the tickets the groups
would pay?
Answers
The reasonable range for the total cost of the tickets the groups
would pay is {84, 126, 2163}.
What is Domain and Range?The sets of all the x-coordinates and all the y-coordinates of ordered pairs, respectively, are the domain and range of a relation.
A function's domain and range are its constituent parts. A function's range is its potential output, whereas its domain is the set of all possible input values.
Given:
The Function modeled for the situation is
f(x) = 21 x where x is the number of tickets sold.
So, For x= 4 Tickets
Fare, F(x) = 21 x 4= $84
and, For x= 6 Tickets
Fare, F(x) = 21 x 6 = $126
and, For x= 103 Tickets
Fare, F(x) = 21 x 103 = $2163.
Hence, the range is {84, 126, 2163}.
Learn more about Domain and Range here:
https://brainly.com/question/28135761
#SPJ1
what is this 1 times 11 =2 times m 45
Answers
Answer:
m = 0.122
Step-by-step explanation:
1 * 11 = 2 *45m
11 = 2*45m
11/2 = 45m
5.5/45 = m
I don't understandthere are 4 polygons that go with the chart

Answers
First four are regular polygons
Last two are, non regular polygons
Then write for
HEXAGON. Degree of rot= 360°/6 = 60°. Reflection lines = 6
SQUARE. Degree of rot= 360°/4 = 90°. Reflection lines= 4
TRIANGLE. Degree of rot= 360°/3= 120°. Reflection lines= 3
PENTAGON. Degree of rot = 360°/5= 72°. Reflection lines= 5
Light waves are electromagnetic waves. This means that there does not need to be a medium for the wave to travel through and that it has a “universal” speed called the "speed of light." If you multiply the speed of light by the period, you get the distance the wave travels during one cycle. This is called the "wavelength." The electromagnetic spectrum given below describes the wavelength pictorially and numerically.
Note how small the visible light spectrum is relative to the entire spectrum. If you were to describe this to someone who did not know trigonometry, what would you say? Does something similar happen for sound waves?

Answers
Sound waves are different from light because they must travel through a material medium.
What is light?Light commonly refers to the sensation that is perceived by our eyes. Beyond that, is a term used to describe electromagnetic radiation. These are waves that contain oscillating electric and magnetic fields.
All these electromagnetic waves travel at the same speed. The time that one cycle of the wave takes to travel is called its period. The product of this period and the velocity of the wave tell us how far the wave can travel horizontally. This is known as the wavelength.
Sound waves are different from light because they must travel through a material medium. The speed of sound is far less tan the speed of light.
Learn more about speed of light:https://brainly.com/question/394103
#SPJ1
Find the value of y.

Answers
The value of y is 4√3
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The corresponding angles of similar triangles are congruent or equal.
Also , the ratio of corresponding sides of similar triangles are equal.
There are two triangles that are similar
Therefore;
y /16 = 4/y
y² = 48
y = √48
y = √16 × √ 3
y = 4√3
Therefore, the value of y is 4√3
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
ANSWER THIS ASAP DONT SEND A FILE AT ALL !! I NEED SO SUBMIT IN 3 MINUTES HELPP!!

Answers
Answer:
(1, -2) is the coordinate of B' after a rotation of 90 degrees
(18) Billy has to read
more than 10 hours
each week. It takes him
30 minutes to finish his
First book. He divides
the remainder of the
time equally amongst
the other
5 days.
What is the minimum
number of minutes he
must read each day?
Answers
Answer:
114
Step-by-step explanation:
Billy has to read more than 10 hours per week, which is equal to 1060=<<1060=600>>600 minutes.
Since it takes him 30 minutes to finish his first book, he has 600-30=<<600-30=570>>570 minutes left.
He needs to divide this time equally amongst the other 5 days, so he must read a minimum of 570/5=<<570/5=114>>114 minutes per day.
List all the 4-tuples in the relation {(a,b,c,d) | a,b,c,d∈!+ , a+b+c+d = 6}
Answers
We have a total of seven 4-tuples that satisfy the given relation.The given relation is {(a,b,c,d) | a,b,c,d∈!+ , a+b+c+d = 6}. It can be understood as the set of 4-tuples (a, b, c, d) such that a, b, c, and d are positive integers and their sum is equal to 6.
Let's now list all the possible 4-tuples that satisfy the given relation. The possible combinations are as follows: (1, 1, 1, 3), (1, 1, 2, 2), (1, 2, 1, 2), (2, 1, 1, 2), (1, 2, 2, 1), (2, 1, 2, 1), and (2, 2, 1, 1).
Here's a brief explanation on how these 4-tuples were obtained. Let a, b, c, and d be positive integers such that a+b+c+d = 6. The least possible value that each variable can take is 1.
So, we start with a=1 and find all possible values of (b, c, d) that satisfy the given equation. Then, we move to a=2 and repeat the process. Finally, we list all the possible 4-tuples that we obtained.
Thus, we have a total of seven 4-tuples that satisfy the given relation.
For more question on integers
https://brainly.com/question/929808
#SPJ8
The sum of two numbers is 20 and the difference of the two numbers is 30. Find both numbers.
Answers
5 and 25.
The problem you've presented is a system of equations. We can use algebraic methods to solve it.Let's call the two natural numbers x and y. According to the information you've provided, we know that:x + y = 30 (the sum of the two numbers is 30)
x - y = 20 (the difference between the two numbers is 20)To find the product of the two numbers, we can multiply them together. So we want to find:x * y = ?To solve for x * y, we'll use the equations we have. We can start by adding the two equations together:(x + y) + (x - y) = 30 + 20
2x = 50
x = 25 Now that we know the value of x, we can substitute it back into one of the original equations to find the value of y:x + y = 30
25 + y = 30
y = 5 So the two natural numbers are 25 and 5. To find the product of the two numbers, we'll multiply them together:x * y = 25 * 5 = 125The product of the two numbers is 125.
05 Algebra Find the missing angle measures in each figure. 26. (x + 11) 24. 25. 95° 124° 749 (x - 13) bo 110° 104° polygon that is not

Answers
The sum of the internal angles of that figure is equal to 720, therefore:
\(\begin{gathered} 90+n+n+n+n+90=720 \\ add_{\text{ }}like_{\text{ }}terms\colon \\ 180+4n=720 \\ solve_{\text{ }}for_{\text{ }}n\colon \\ 4n=720-180 \\ 4n=540 \\ n=\frac{540}{4} \\ n=135 \end{gathered}\)4 children each have some beads, the mean number of beads is 8 Rajiv brings some more beads. The mean number of 5 children is now 9 what is the numberx of beads Rajiv brings
Answers
Answer:
The number of beads Rajiv brings is: 13Step-by-step explanation:
Make a plan:In this question, we need to use the formula of means to solve the. We can set the number of beads Rajiv brings as X, and use the formula of mean to get the total number of beads that the Four(4) children have and the total number of beads that the Five(5) children have.
Solve the problem:Four(4) children each have some beads, the mean number of beads is: 8
We can get the total number of beads the Four(4) children have:4 * 8 = 32
Rajiv brings some more beads:We set the number of beads Rajiv brings as:
x, so the total number of beads that the Five(5) children have is:
32 + x
The mean number of the Five(5) children is now: 9
We can get the total number of beads that the Five(5) children have:5 * 9 = 45
Now, we have the equation:32 + x = 45
x + 32 = 45
- 32 = -32
x = 13
By solving the above equation, you can get:
x = 13
Hence, The number of beads Rajiv brings is:13
Hope this helps!
Consider the following symbolic logic statement: ¬ (∃x)(P(x) ∧ Q(x)) ∧ (∀y)(R(y) → P(y))
a) Translate the statement into English using proper syntax and semantics.
b) Identify and explain any potential ambiguities in the translated statement.
c) Rewrite the statement in a way that eliminates any ambiguities and maintains the original meaning.
Answers
(a). The statement can be translated into English as follows "Not exists x such that P(x) and Q(x), and for all y, if R(y) then P(y)." (b) The rewritten statement explicitly places the negation symbol "¬" only in front of the existential quantifier (∃x). (c). This clarifies that the negation applies to the existence of x such that P(x) and Q(x).
a) Translation into English:
The statement can be translated into English as follows:
"Not exists x such that P(x) and Q(x), and for all y, if R(y) then P(y)."
b) Potential ambiguities in the translated statement:
Ambiguity in the scope of negation: The placement of the negation symbol "¬" might lead to ambiguity. It is not clear whether the negation applies only to the existential quantifier (∃x) or to the entire statement. Specifically, it is unclear if the negation applies to both conjuncts separately or to their conjunction as a whole.
Ambiguity in the scope of quantifiers: The scope of the quantifiers (∃x) and (∀y) is not explicitly defined. It is unclear which variables the quantifiers bind to and how they relate to the predicates P(x), Q(x), R(y), and P(y).
c) Rewritten statement to eliminate ambiguities while maintaining the original meaning:
To eliminate the ambiguities, we can rewrite the statement as follows:
(¬∃x)(P(x) ∧ Q(x)) ∧ (∀y)(R(y) → P(y))
The rewritten statement explicitly places the negation symbol "¬" only in front of the existential quantifier (∃x). This clarifies that the negation applies to the existence of x such that P(x) and Q(x). Additionally, parentheses are used to explicitly define the scope of the quantifiers (∃x) and (∀y), making it clear which variables they bind to.
For more such questions on symbol , Visit:
https://brainly.com/question/30289310
#SPJ11
Help, please
f(n)=3(n+2)^2 (n-3) (n-2)
As n -----> -oo, f(n)----> ?
As n ----->oo, f(n) ----->?
Answers
The end behavior of the function f(n) = 3(n + 2)²(n - 3)(n - 2) is given as follows:
As n -> -oo, f(n) -> oo.As n -> oo, f(n) -> +oo.What is the end behavior of a function?The end behavior of a function refers to how the function behaves as the input variable approaches positive or negative infinity.
The function for this problem is given as follows:
f(n) = 3(n + 2)²(n - 3)(n - 2).
Considering the degree, the function can be interpreted as follows:
\(3n^4\)
(for the limit when the input goes to infinity we consider only the term with the highest degree).
The leading coefficient is positive and the exponent is even, hence the end behavior is given as follows:
As n -> -oo, f(n) -> oo.As n -> oo, f(n) -> +oo.More can be learned about the end behavior of a function at brainly.com/question/1365136
#SPJ1
Add (7.8 x 10^5) + (2.4 x 10^5).
Answers
\((7.8*10^5)+(2.4 * 10^5)\)
\((7.8 * 100,000) + (2.4 * 100,000)\)
\(780,000 + 240,000\)
= 1,020,000
Answer:
1020000
Step-by-step explanation:
(7.8 x 10^5) + (2.4 x 10^5)
780000+240000
1020000
Hopes this helps please mark brainliest
which is the correct answer?

Answers
Step-by-step explanation:
Step 3 is incorrect, it should be x - 4 + x = x(x - 3).
x - 4 + x = x(x - 3)
2x - 4 = x² - 3x
x² - 5x + 4 = 0
(x - 4)(x - 1) = 0
x = 4 or x = 1.
x = 4 is rejected as 1 / (x - 4) will become 1 / 0 which is undefined.
=> x = 1.
Morganton Company makes one product and it provided the following information to help prepare the master budget:
The budgeted selling price per unit is $60. Budgeted unit sales for June, July, August, and September are 8,600, 17,000, 19,000, and 20,000 units, respectively. All sales are on credit.
Thirty percent of credit sales are collected in the month of the sale and 70% in the following month.
The ending finished goods inventory equals 25% of the following month’s unit sales.
The ending raw materials inventory equals 10% of the following month’s raw materials production needs. Each unit of finished goods requires 5 pounds of raw materials. The raw materials cost $2.40 per pound.
Thirty five percent of raw materials purchases are paid for in the month of purchase and 65% in the following month.
The direct labor wage rate is $14 per hour. Each unit of finished goods requires two direct labor-hours.
The variable selling and administrative expense per unit sold is $1.80. The fixed selling and administrative expense per month is $67,000.
5. If 96,250 pounds of raw materials are needed to meet production in August, how many pounds of raw materials should be purchased in July?
Answers
Raw materials purchases in July - Payment for raw materials purchases in July = Desired ending raw materials inventory for July
X pounds - 0.35 * X pounds = 9,500 pounds
Solving this equation will give us the value of X, which represents the pounds of raw materials that should be purchased in July.
To determine the number of pounds of raw materials that should be purchased in July, we need to calculate the raw materials production needs for August and then consider the inventory policies given in the information provided.
Each unit of finished goods requires 5 pounds of raw materials. The budgeted unit sales for August are 19,000 units. Therefore, the raw materials production needs for August would be 19,000 units multiplied by 5 pounds per unit, which equals 95,000 pounds.
The ending raw materials inventory equals 10% of the following month’s raw materials production needs. Therefore, the desired ending raw materials inventory for July would be 10% of 95,000 pounds, which is 9,500 pounds.
To calculate the raw materials purchases for July, we need to consider the payment terms provided. Thirty-five percent of raw materials purchases are paid for in the month of purchase and 65% in the following month.
Let's assume the raw materials purchases for July are X pounds. Then the payment for 35% of X pounds will be made in July, and the payment for 65% of X pounds will be made in August.
The payment for raw materials purchases in July (35% of X pounds) will be:
0.35 * X pounds
The payment for raw materials purchases in August (65% of X pounds) will be:
0.65 * X pounds
Since the raw materials purchases for July should cover the desired ending raw materials inventory for July (9,500 pounds), we can set up the following equation:
Raw materials purchases in July - Payment for raw materials purchases in July = Desired ending raw materials inventory for July
X pounds - 0.35 * X pounds = 9,500 pounds
Solving this equation will give us the value of X, which represents the pounds of raw materials that should be purchased in July.
for such more question on equation
#SPJ8
HELP I WILL GIVE BRAINLIEST IF RIGHT

Answers
Answer:
a
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
I might be wrong but i'm pretty sure it's right
.5% of what number is 15.8?
Answers
Answer:
316 should be your answer
Step-by-step explanation:
Answer:
3160
Step-by-step explanation:
.5% of what number is 15.8?
Let the unknown number be x.
0.5% * x = 15.8
0.005x = 15.8
x = 15.8/0.005
x = 3160
Write these fractions as whole nombers
8/4
21/3
56/8
48/8
Answers
Answer:2, 7, 7, 6
Step-by-step explanation:
Answer:
1) 8/4 = 2
2) 21/3 = 7
3) 56/8 = 7
4) 48/8 = 6
Step-by-step explanation:
To convert a fraction into a whole number: Divide the numerator by the denominator.
What's a numerator?:
A numerator is the part of a fraction above the line. So, 8 in 8/4 is the numerator.
What's a denominator?:
A denominator is the bottom number in a fraction. So, 4 in 8/4 is the denominator.
1) 8/4 = 8 divided by 4 = 2.
2) 21/3 = 21 divided by 3 = 7
3)56/ 8 = 56 divided by 8 = 7
4) 48 / 8 = 48 divided by 8 = 6
PLS HELP!!! due to inflation nominal prices are usually there were to demand increases. After the second increase the price for a certain item was twice as big as the original. By what percent was the first increase, if the second increase was 25%
Answers
Answer:
The first increase was of 60%.
Step-by-step explanation:
The initial value of the product is x.
The first increase was of y.
The second increase is of 25%, that is, 1.25.
The final price was double the original, so 2x.
This situation can be modeled by the following equation:
\(xy(1.25) = 2x\)
We want to find y.
Simplifying by x
\(1.25y = 2\)
\(y = \frac{2}{1.25}\)
\(y = 1.6\)
After the first increase, the value was 1.6 of the original value, that is a increase as a percent of (1.6 - 1)*100 = 60%.
HELP!!!!!!!! Which system of linear equations can be solved using the information below?

Answers
The system of linear equations that can be solved from the matrices is given as follows:
-5x + 4y = 3.-8x + y = -6.How to obtain the system of equations?Considering that the row [3, -6] is common to matrices Ax and Ay, the matrix A is given as follows:
A = [-5 4; -8 1]
Hence the multiplication of matrices representing the system is given as follows:
[-5 4; -8 1][x; y] = [3; -6]
Applying the multiplication of matrices, the system of equations is given as follows:
-5x + 4y = 3.-8x + y = -6.More can be learned about a system of equations at https://brainly.com/question/13729904
#SPJ1
Calculate the range, population variance, and population standard deviation for the following data set. If necessary, round to one more decimal place than the largestnumber of decimal places given in the data.9, 10, 11, 12, 13, 14, 15, 16, 17, 18Copy DataAnswerHow to enter your answer (opens in new window)Range:Population Variance:Population Standard Deviation:KeypacKeyboard ShortcuTables

Answers
Given: The data below
\(9,10,11,12,13,14,15,16,17,18\)To Determine: The range, population variance and population standard deviation
Solution
The range of a data set is the difference between the largest number and the smallest number in the data set. Therefore
\(\begin{gathered} Range=18-9 \\ Range=9 \end{gathered}\)The population variance of a data set can be calculated using the formula below
\(\begin{gathered} Variance(s^2)=\frac{1}{n}\Sigma(x-\bar{x})^2 \\ n=Total-number \\ \bar{x}=mean \end{gathered}\)\(\bar{x}=\frac{9+10+11+...+18}{10}=\frac{135}{10}=13.5\)\(Variance(s^2)=\frac{(9-13.5)^2+(10-13.5)^2+...+(18-13.5)^2}{10}\)\(Variance(s^2)=\frac{82.5}{10}=8.25\)The population standard deviation is
\(\begin{gathered} Population-standard-devation(s)=\sqrt{Population-variance} \\ s=\sqrt{8.25} \\ s=2.872 \\ s\approx2.9 \end{gathered}\)Hence:
Range = 9
Population variance = 8.25
Population standard deviation = 2.9
Has anyone done the inverse functions mastery text on edmentum it’s super hard stuck on this question and the pictures wont help
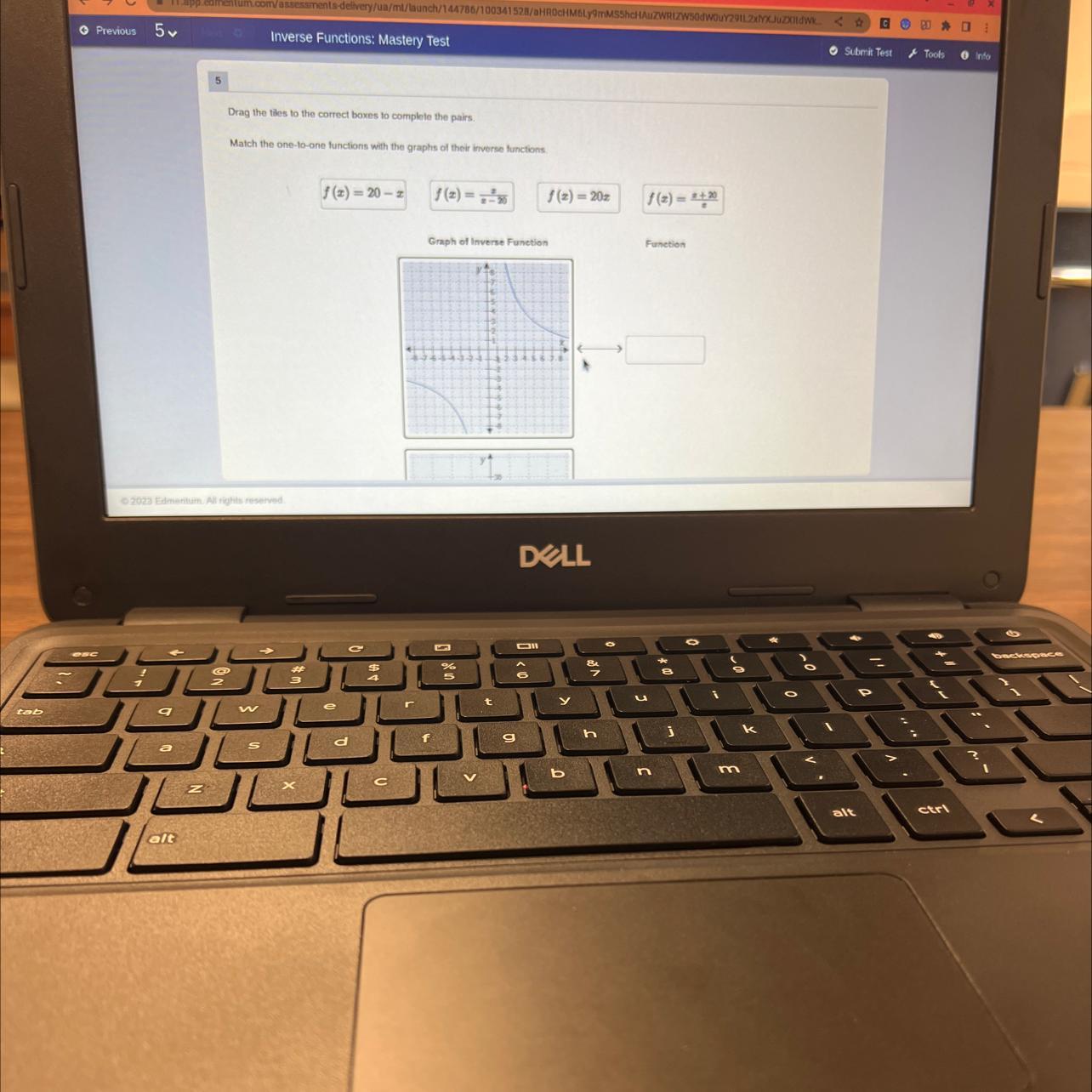
Answers
Find all points on the curve x^2y^2+xy=2 where the slope of the tangent line is −1
Answers
Differentiate both sides with respect to x and solve for the derivative dy/dx :
\(\dfrac{\mathrm d}{\mathrm dx}\left[x^2y^2+xy\right] = \dfrac{\mathrm d}{\mathrm dx}[2] \\\\ \dfrac{\mathrm d}{\mathrm dx}\left[x^2\right]y^2 + x^2\dfrac{\mathrm d}{\mathrm dx}\left[y^2\right] + \dfrac{\mathrm d}{\mathrm dx}\left[x\right]y + x\dfrac{\mathrm dy}{\mathrm dx} = 0 \\\\ 2xy^2 + x^2(2y)\dfrac{\mathrm dy}{\mathrm dx} + y + x\dfrac{\mathrm dy}{\mathrm dx} = 0 \\\\ (2x^2y+x)\dfrac{\mathrm dy}{\mathrm dx} = -2xy^2-y \\\\ \dfrac{\mathrm dy}{\mathrm dx} = -\dfrac{2xy^2+y}{2x^2y+x}\)
This gives the slope of the tangent to the curve at the point (x, y).
If the slope of some tangent line is -1, then
\(-\dfrac{2xy^2+y}{2x^2y+x} = -1 \\\\ \dfrac{2xy^2+y}{2x^2y+x} = 1 \\\\ 2xy^2+y = 2x^2y+x \\\\ 2xy^2-2x^2y + y - x = 0 \\\\ 2xy(y-x)+y-x = 0 \\\\ (2xy+1)(y-x) = 0\)
Then either
\(2xy+1 = 0\text{ or }y-x=0 \\\\ \implies y=-\dfrac1{2x} \text{ or }y=x\)
In the first case, we'd have
\(x^2\left(-\dfrac1{2x}\right)^2+x\left(-\dfrac1{2x}\right) = \dfrac14-\dfrac12 = -\dfrac14\neq2\)
so this case is junk.
In the second case,
\(x^2\times x^2+x\times x=x^4+x^2=2 \\\\ x^4+x^2-2 = (x^2-1)(x^2+2)=0\)
which means either
\(x^2-1 = 0 \text{ or }x^2+2 = 0 \\\\ x^2 = 1 \text{ or }x^2 = - 2\)
The second case here leads to non-real solutions, so we ignore it. The other case leads to \(x=\pm1\).
Find the y-coordinates of the points with x = ±1 :
\(x=1 \implies y^2+y=2 \implies y=-2 \text{ or }y=1 \\\\ x=-1\implies y^2-y=2\implies y=-1\text{ or }y=2\)
so the points of interest are (1, -2), (1, 1), (-1, -1), and (-1, 2).
What is the answer to this problem?

Answers
Answer:
The volume of hemisphere = 2/3 pie r ^3
or, 18 pie = 2/3 pie r ^ 3
or, 27 = r ^ 3
or, r = 3 inches #
hope this helps
All the best!!
Each letter of the word BANANA is written on a card. Find each probability if you pick two cards without replacing the first. Assume that you get the letter you want when you draw.
4. P (B and then A)
5. P (N and then N)
6. P (B and then a B
Answers
Answer:
5
Step-by-step explanation:
There answer would be 5
Which of the following is most likely the next step in the series?
)DO
O A.
• B.
•

Answers
Following the pattern, the most likely next step in the series is given by the pentagon in option B.
What is the most step for the series?We have to look at the number of points in each figure, hence:
The first figure, with the line segment, has two points.The second figure, with the triangle, has three points.The fourth figure, with the rectangle has four points.Hence, the number of points increases by one for each figure, meaning that in the next step, the figure should have 5 points, representing a pentagon.
Among the options given for the answer, only one, option B, has 5 points, with the pentagon, as:
Option A has one point.Option C has four points.Option D has three points.Hence, the most likely next step in the series is given by the pentagon in option B.
More can be learned about patterns at https://brainly.com/question/27033681
#SPJ1
Identify the pivot positions in the original matrix. The pivot positions are indicated by bold values. Choose the correct answer below.A.1 2 3 43 4 5 65 6 7 8B.1 2 3 43 4 5 65 6 7 8C.1 2 3 43 4 5 65 6 7 8D.1 2 3 43 4 5 65 6 7 8
Answers
The pivot positions of the matrix are 1, 3, 5, and 7.
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.
In this case, all the given options (A, B, C, and D) contain the same numbers and have the same structure, so we can examine any one of them to determine the pivot positions.
The pivot positions in the given matrix can be found as follows:
The first pivot position is in the first row, first column (1).
The second pivot position is in the second row, second column (3).
The third pivot position is in the third row, third column (5).
The fourth pivot position is in the fourth row, fourth column (7).
So, the pivot positions in the matrix are 1, 3, 5, and 7. These are the bold values in the matrix and indicate the leading entries after row operations have been performed.
Complete Question:
Identify the pivot positions in the original matrix. The pivot positions are indicated by bold values. Choose the correct answer below.
A.1 2 3 4 3 4 5 6 5 6 7 8
B.1 2 3 4 3 4 5 6 5 6 7 8
C.1 2 3 4 3 4 5 6 5 6 7 8
D.1 2 3 4 3 4 5 6 5 6 7 8
To know more about matrix here.
https://brainly.com/question/28180105
#SPJ4
Use the eigenvalue method to solve the following system of equations X1(0) = 3 x2(0) = 3X1' = -13x1 + 9x2 X2' = -5x1 + x2Next, use the following initial conditions to determine the corresponding particular solution to the above system of differential equations.
Answers
The corresponding particular solution to the system of differential equations :
X(t) = -6e^(-12t)(1, 1) + 6e^(2t)(3, -1)
The EigenvalueThe eigenvalue method involves finding the eigenvalues and eigenvectors of the matrix associated with the system of differential equations.
First, we can write the system of differential equations in matrix form as follows:X' = AX
where X is a column vector with the variables x1 and x2,
X' is the derivative of X with respect to t,
and A is the coefficient matrix given by:
A = [ -13 9
-5 1 ]
Next, we find the eigenvalues and eigenvectors of the matrix A. The characteristic equation is given by:det(A - λI) = 0
where I is the identity matrix and λ is an eigenvalue.
Solving for the eigenvalues, we find:λ = -12, 2
For each eigenvalue, we solve for the corresponding eigenvector by setting up a system of equations and solving for the unknowns. For λ = -12, the eigenvector is (1, 1), and for λ = 2, the eigenvector is (3, -1).
Next, we write the general solution to the system of differential equations as:X(t) = c1e^(-12t)u1 + c2e^(2t)u2
where c1 and c2 are constants and u1 and u2 are the eigenvectors corresponding to the eigenvalues -12 and 2, respectively.
Finally, we use the initial conditions to find the particular solution. We have X1(0) = 3 and x2(0) = 3, so we can write:X(0) = [3 3] = c1u1 + c2u2
Solving for the constants c1 and c2, we find:c1 = -6, c2 = 6
So the particular solution to the system of differential equations with the given initial conditions is:X(t) = -6e^(-12t)(1, 1) + 6e^(2t)(3, -1)
This is the final solution to the system of differential equations.
Learn more about The Eigenvalue here:
https://brainly.com/question/29749542
#SPJ4
john has a rectangular shaped figure shoes length is 62.5 yards and width is 45.3 yards The area of the field is 2,731.25 square yards the perimeter of the field is blank yards
