Find the slope of the line for the points (8.18) and (2,12)
Answers
Answer:
m=1
Step-by-step explanation:
(8,18);(2,12)
(x1,y1)=(8,18)
(x2,y2)=(2,12)
Use the slope formula:
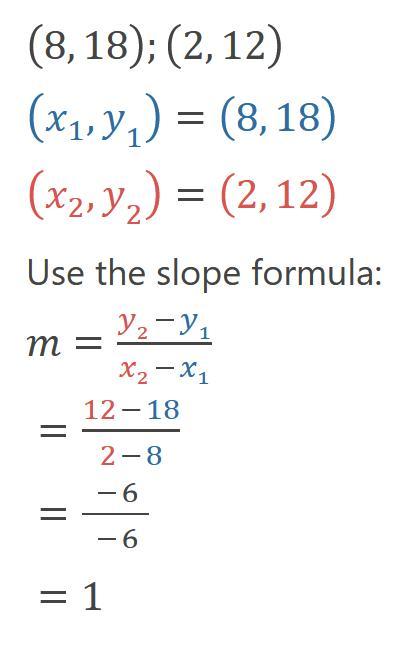
Related Questions
Help open up a jewelry store, Tom borrowed money from an online lending company He took out a personal, amortized loan for 44,000, at an interest rate of 6. 25\% with monthly payments for a term of 7 years For each part, do not round any intermediate computations and round your final answers to the nearest cent necessary, refer to the list of financial formulas (a) Find Tom's monthly payment (b) Tom pays the monthly payment each month for the full term , his total amount to repay the () Tom pays the monthly payment each month for the full termfind the total amount of interest he will pay
Answers
Tom will pay a total of $13,424.20 in interest over the term of the loan.
The formula to calculate the monthly payment for an amortized loan is given by: `P = r(PV) / [1 - (1 + r)^(-n)]`Where P is the monthly payment, r is the interest rate per month, PV is the present value of the loan, and n is the number of payments or the total number of months.
Substituting the given values, we get:P = 0.0052083333 × 44,000 / [1 - (1 + 0.0052083333)^(-7×12)]P = 632.32Therefore, Tom's monthly payment is $632.32 (rounded to the nearest cent).b. Since Tom pays the monthly payment each month for the full term, his total amount to repay the loan is equal to the present value of the loan.
Therefore, the total amount to repay the loan is $44,000 (rounded to the nearest cent).c. The total amount of interest paid over the term of the loan can be calculated as the difference between the total amount repaid and the principal amount of the loan.
Therefore, the total interest paid is: Total interest paid = Total amount repaid - Principal amount of the loan Total interest paid = $57,424.20 - $44,000Total interest paid = $13,424.20
For more questions on monthly payment
https://brainly.com/question/27926261
#SPJ11
Find each indefinite integral: 1. ∫sec 5(πx)tan(πx)dx
Answers
The indefinite integral of ∫sec^5(πx)tan(πx)dx is (1/4)sec^3(πx) + C, where C is the constant of integration. This can be obtained by applying integration techniques such as substitution and power rule.
To evaluate the indefinite integral, we can use the technique of substitution. Let u = πx, then du/dx = π, and dx = du/π. Substituting these values into the integral, we have:
∫sec^5(πx)tan(πx)dx = ∫sec^5(u)tan(u)(du/π)
Now we have transformed the integral with respect to u. We can simplify further by using trigonometric identities. Recall that sec^2(u) = 1 + tan^2(u). Rearranging this identity, we get tan^2(u) = sec^2(u) - 1. Multiplying both sides by sec^3(u), we have tan^2(u)sec^3(u) = sec^5(u) - sec^3(u).
Substituting this result into our integral expression, we have:
∫sec^5(u)tan(u)(du/π) = (1/π)∫[sec^5(u) - sec^3(u)](tan(u)du)
Now we can split this into two separate integrals:
(1/π)∫sec^5(u)tan(u)du - (1/π)∫sec^3(u)tan(u)du
For the first integral, we can apply the power rule of integration. Letting v = sec(u), then dv = sec(u)tan(u)du. The integral becomes:
(1/π)∫v^5dv = (1/π)(1/6)v^6 + C1
Replacing v with sec(u), we have:
(1/π)(1/6)sec^6(u) + C1
For the second integral, we can use a similar substitution. Let w = sec(u), then dw = sec(u)tan(u)du. The integral becomes:
(1/π)∫w^3dw = (1/π)(1/4)w^4 + C2
Replacing w with sec(u), we have:
(1/π)(1/4)sec^4(u) + C2
Combining the results, we obtain:
∫sec^5(πx)tan(πx)dx = (1/π)(1/6)sec^6(u) - (1/π)(1/4)sec^4(u) + C
Simplifying further, we get:
(1/4)sec^3(πx) + C
Therefore, the indefinite integral of ∫sec^5(πx)tan(πx)dx is (1/4)sec^3(πx) + C, where C is the constant of integration.
To learn more about indefinite integral click here: brainly.com/question/31549816
#SPJ11
What is 98% of £7
Please help ASAP
Answers
Answer:
£6.86
Step-by-step explanation:
10%=0.7
0.75*98=6.86
Answer:
£6.86
Step-by-step explanation:
98% × 7
0.98 × 7
= 6.86
98% of £7 is £6.86.
someone help pls ;-; im lost

Answers
The formula of a circle is A=pi x radius^2
i cant see the blue and red numbers for some reason ill do the other 4 by plugging them in
yellow:153,94 rounded 153,9
green:1385.4
orange3019.1
purple:227
circumference formula c=2 X pi X r
yellow: 43.9
green: 132
orange: 194.8
purple: 53.4
plz correct me if im wrong
Sarah will have seven test scores. Each of the scores is an integer value. The first five scores are 82, 87, 92, 9682,87,92,96 and 9898. How many distinct values are possible for the median of Sarah's seven scores once she takes the last two tests
Answers
We can see that there are two distinct values possible for the median of Sarah's seven scores: 92 and 96.
To determine the number of distinct values possible for the median of Sarah's seven scores, we need to consider all possible combinations of the last two test scores and calculate the median for each combination.
Given the first five scores: 82, 87, 92, 96, and 98, there are a total of 5!/(2!(5-2)!) = 10 possible arrangements of these scores.
Let's calculate the median for each arrangement:
Arrange: 82, 87, 92, 96, 98
Median: 92
Arrange: 82, 87, 92, 98, 96
Median: 92
Arrange: 82, 87, 96, 92, 98
Median: 92
Arrange: 82, 87, 96, 98, 92
Median: 96
Arrange: 82, 87, 98, 92, 96
Median: 92
Arrange: 82, 87, 98, 96, 92
Median: 96
Arrange: 82, 92, 87, 96, 98
Median: 92
Arrange: 82, 92, 87, 98, 96
Median: 92
Arrange: 82, 92, 96, 87, 98
Median: 92
Arrange: 82, 92, 96, 98, 87
Median: 96
From the above calculations, we can see that there are two distinct values possible for the median of Sarah's seven scores: 92 and 96.
Learn more about median here:
https://brainly.com/question/300591
#SPJ11
Is thh huh is the correct answer

Answers
Answer:
ya your right can i please get brainliest i need two more to get the next rank
Step-by-step explanation:
Answer:
yes.
Step-by-step explanation:
you are correct
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP

Answers
i need help please help

Answers
Answer:it is C
Step-by-step explanation:
I need help solving this

Answers
Answer:
AD ≈ 80
Step-by-step explanation:
The Pythagorean theorem can be used to write and solve relations between the various edges and diagonals.
AE is the hypotenuse of ΔABE, so you have ...
AE² = AB² +BE²
BE² = AE² -AB² = 65 -52 = 13
__
AD is the hypotenuse of ΔACD. We presume the figure is a rectangular prism, so CD = BE. Then you have ...
AD² = AC² +CD²
AD² = 80² +13 = 6413 . . . . . CD² = BE² = 13
AD = √6413 ≈ 80.081
AD ≈ 80
answers are
60m cubed
360m cubed
1130m cubed
2260m cubed

Answers
Answer:
≈ 1130 m³
Step-by-step explanation:
The volume (V) of a cylinder is calculated as
V = πr²h ( r is the radius and h the height )
Here r = 6 and h = 10 , then
V = π × 6² × 10 = π × 36 × 10 = 360π ≈ 1130 m³
Pls help me out with this!!!


Answers
The correct formula for the expression is,
⇒ f (x) = - 6 cos (π/4.5x - 2π) + 2
Since, Trigonometry is a branch of mathematics that deals with the relationship between sides and angles of a right-angle triangle.
We have a function:
f(x) = a cos(bx + c) + d
Here a is the amplitude:
Since, The value of d is the average of maximum and minimum.
Hence, d = (9 - 5)/2 = 4/2 = 2
And, The value of 'a' is the difference between the maximum value and d.
Hence, a = -4 -(2) = - 6
Here, the half-period is,
= π - 3π/4) = π/4
= b = 2π/9 = π/4.5
The value of c is the value makes the cosine zero at x= 9
⇒ (π/4.5)(9) +c = 0
⇒ c = -2π
Hence, Function is,
f (x) = - 6 cos (π/4.5x - 2π) + 2
Learn more about trigonometry here:
brainly.com/question/26719838
#SPJ1
Answer:
The correct answer would be:
f (x) = - 6 cos (π/4.5x - 2π) + 2
PLEASE HELP ME I WILL GIVE 36 POINTS PLEASE RIGHT ANSWER FIRST RIGHT ANSWER GETS THE 36 POINTS AND BRAINLIESET!

Answers
Answer
\(592in^{2}\)
Step-by-step explanation:
A=2(wl+hl+hw)
2·(10·8+12·8+12·10)
=592
Answer: 592
Step-by-step explanation:
so A = 2 (wl+hl+hw)
Then what we will do next is do 2·(10·8+12·8+12·10)
which will give us 592 and that is our answer.
I hope this helps!
number 5 goes through the device and the result is 25 . what would a possible rule for machine B be ?
Answers
Answer: multiplied by 5 or squared
Step-by-step explanation:
If the number 5 goes in and 25 is the result, the rule could be multiplying by 5 or squaring the number that goes in (input).
5 x 5 = 25
5^2 = 25.
In AJKL, solve for x.

Answers
Answer:
x ≈ 66.73
Step-by-step explanation:
Using the tangent ratio in the right triangle
tan27° = \(\frac{opposite}{adjacent}\) = \(\frac{KL}{JK}\) = \(\frac{34}{x}\) ( multiply both sides by x )
x × tan27° = 34 ( divide both sides by tan27° )
x = \(\frac{34}{tan27}\) ≈ 66.73 ( to 2 dec. places )
more easy math for points

Answers
Answer:
4096
Step-by-step explanation:
Math
Can someone help me PLZ! I keep posting the same question and no ones helping me :((((((((((((
Which step could you use to start solving the system of equations below?
x + y = 3
-3x - 2y = -7
Group of answer choices
Multiply -3x - 2y = -7 by 2 and subtract it from x + y = 3
All of the above.
Multiply x + y = 3 by 3 and add it to -3x - 2y = -7
Add x + y = 3 to -3x - 2y = -7
Answers
Answer:
Multiply x + y = 3 by 3 and add it to -3x - 2y = -7
Step-by-step explanation:
When using elimination to solve a system of equations, you multiply one equation by some number. The reason for doing this is that when you add it to the second equation, you want one variable to cancel out. When one variable cancels out (in this case x), you can solve for the other variable (in this case y). I will show this:
3(x + y = 3) = 3x + 3y = 9
3x + 3y = 9
+ -3x + -2y = -7
---------------------------
y = 2
Now, knowing that y = 2, you can substitute y=2 into either equation to solve for x.
-3x - 2(2) = -7
-3x -4 = -7
-3x = -3
x = 1 | to double check (1, 2) as your answer plug these values into both equations
Finding this solution would not have been possible if not for cancelling out the x's above. The other three are wrong because none of the other options cancels out one of the variables.
Select the true statements.1.Over the interval [2, 3], the average rate of change of g is lower than that of both f and h.2.As x increases on the interval [0, ∞), the rate of change of f eventually exceeds the rate of change of both g and h.3.When x > 4, the value of f(x) exceeds the values of both g(x) and h(x).4.As x increases on the interval [0, ∞), the rate of change of g eventually exceeds the rate of change of both f and h.5.When x ≈ 8, the value of h(x) exceeds the values of both f(x) and g(x).6.A quantity increasing exponentially eventually exceeds a quantity growing quadratically or linearly.
![Select the true statements.1.Over the interval [2, 3], the average rate of change of g is lower than](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/2IFH3wvZSrhj0qvFWNg8FQFDJroSgi71.jpeg)
Answers
Let's check each of the given statements:
1. Over the interval [2, 3], the average rate of change of g is lower than that of both f and h.
The statement is FALSE. The average rate of change of g is HIGHER than f and h.
2. As x increases on the interval [0, ∞), the rate of change of f eventually exceeds the rate of change of both g and h.
The statement is TRUE. f will exceed the rate of change of both g and h exponentially.
3. When x > 4, the value of f(x) exceeds the values of both g(x) and h(x).
Let's try to determine the value at x = 5 on each function to see if it's true.
\(\text{ f(5) = }3^5\text{ + 2 = 245}\)\(\text{ g(5) = }20(5)\text{ + 4 = }100\text{ + 4 = 104}\)\(\text{ h(5) = }2(5)^2\text{ + }5(5)\text{ + }2\text{ = 50 + 25 + 2 = 77}\)Therefore, the statement is TRUE.
4. As x increases on the interval [0, ∞), the rate of change of g eventually exceeds the rate of change of both f and h.
The statement is FALSE. f will exceed the rate of change of both g and h exponentially.
5. When x ≈ 8, the value of h(x) exceeds the values of both f(x) and g(x).
The statement is FALSE. f will exceed the values of both g(x) and h(x) at x = 8.
6. A quantity increasing exponentially eventually exceeds a quantity growing quadratically or linearly.
The statement is TRUE. Proof on the statement 3 example.
Therefore, only Statements 2, 3 and 6 are TRUE.
find the general solution of the given differential equation. y' + 7x^6y = x^6
Answers
The general solution of the given differential equation is:
y = (1/7) + C * \(exp(-x^7)\)
The exponential of the integral of the coefficient of y, in this case 7x6, provides the integrating factor. The integrating factor is given by the exponential of the integral of the coefficient of y, which in this case is 7x⁶.
The integrating factor is therefore exp(∫ 7x⁶ dx), which can be calculated as exp(x⁷/7).
Multiplying both sides of the differential equation by the integrating factor, we have:
exp(x⁷/7) * y' + 7x⁶ * exp(x⁷/7) * y = x⁶ * exp(x⁷/7)
Using the product rule on the left side, we can rewrite the equation as:
d/dx (exp(x⁷/7) * y) = x⁶ * exp(x⁷/7)
Integrating both sides with respect to x, we get:
exp(x⁷/7) * y = ∫ x⁶ * exp(x⁷/7) dx
The integral on the right side can be solved using integration by parts. Let's denote u = x⁶ and dv = exp(x⁷/7) dx. Then, du = 6x⁵ dx and v = 7/7 * exp(x⁷/7) = exp(x⁷/7).
Using the formula for integration by parts:
∫ u dv = uv - ∫ v du
We have:
∫ x⁶ * exp(x⁷/7) dx = x⁶ * exp(x⁷/7) - ∫ exp(x⁷/7) * 6x⁵ dx
Simplifying the integral on the right side, we obtain:
∫ exp(x⁷/7) * 6x⁵ dx = 6 * ∫ x⁵ * exp(x⁷/7) dx
We can apply integration by parts again to this integral, with u = x⁵ and dv = exp(x⁷/7) dx.
Continuing this process, we will eventually reach an integral of the form ∫ exp(x⁷/7) dx, which can be expressed in terms of special functions called exponential integrals.
Once we have the value of this integral, we can substitute it back into the expression for the integral of x⁶ * exp(x⁷/7) dx.
Finally, we divide both sides of the equation by exp(x⁷/7) and solve for y:
y = (1/exp(x⁷/7)) * (∫ x⁶ * exp(x⁷/7) dx)
The resulting expression will give the general solution to the given differential equation.
To solve this linear first-order ordinary differential equation, we can use an integrating factor. The integral of the coefficient of y's exponential integral, in this case 7x⁶, provides the integrating factor.
The integrating factor is therefore exp(∫ 7x⁶ dx), which can be calculated as exp((7/7) * x⁷) = exp(x⁷).
Multiplying both sides of the differential equation by the integrating factor, we have:
exp(x⁷) * y' + 7x⁶ * exp(x⁷) * y = x⁶ * exp(x⁷)
We can rewrite this equation as follows:
d/dx (exp(x⁷) * y) = x⁶ * exp(x⁷)
Integrating both sides with respect to x, we get:
exp(x⁷) * y = ∫ x⁶ * exp(x⁷) dx
To evaluate this integral, we can make a substitution. Let's substitute u = x⁷, then du = 7x⁶ dx.
The integral becomes:
(1/7) ∫ exp(u) du = (1/7) * exp(u) + C = (1/7) * exp(x⁷) + C
Now, dividing both sides of the equation by exp(x⁷), we have:
y = (1/7) + C * exp(-x⁷)
Therefore, the general solution of the given differential equation is:
y = (1/7) + C * exp(-x⁷)
where C is an arbitrary constant.
To know more about integration follow the given link:
https://brainly.com/question/30094386
#SPJ4
_____ is used to test the hypothesis that the values of the regression parameters β1, β2, . . . , βq are all zero.
a. An F test b. A t test c. The least squares method d. Extrapolation
Answers
An F test is used to test the hypothesis that the values of the regression parameters β1, β2, . . . , βq are all zero. So the correct option is A.
The F test is based on the ratio of the mean square of the regression to the mean square of the error, and it is used to test the overall significance of the regression model. It tests whether there is a linear relationship between the independent variables and the dependent variable, and whether the model is statistically significant. In contrast, a t test is used to test the significance of individual regression coefficients, and the least squares method is a technique used to estimate the parameters of a linear regression model. Extrapolation is the process of estimating values of a dependent variable outside the range of the independent variables based on the regression model.
Learn more about hypothesis ,
https://brainly.com/question/29519577
#SPJ4
The F test is used to test the hypothesis that the values of the regression parameters β1, β2, . . . , βq are all zero. therefore, option a. an F text is correct.
This test is commonly used in regression analysis to determine whether there is a significant relationship between the
dependent variable and the independent variables.
The F test compares the variance explained by the regression model to the residual variance, and the null hypothesis
assumes that all regression coefficients are equal to zero, indicating no relationship between the dependent variable
and the independent variables.
If the calculated F-statistic is larger than the critical value, we reject the null hypothesis and conclude that there is a
significant relationship between the dependent variable and the independent variables.
for such more question on F test
https://brainly.com/question/17256783
#SPJ11
In ssa case for an obtuse angle, what is the maximum number of triangles that can be generate with the given information?.
Answers
Using the SSA method, the maximum number of triangles that can be generate is 1.
In the given question,
In SSA case for an obtuse angle, we have to find the maximum number of triangles that can be generate with the given information.
As we know that,
There cannot be a second obtuse angle if the specified first angle is already obtuse since the triangle's angle total would be greater than 180°. As a result, there is only one way to construct the triangle, making SSA a valid congruence theorem when the supplied angle is acute.
So the maximum number of triangles that can be generate is 1.
To learn more about SSA method link is here
brainly.com/question/10582575
#SPJ4
a dozen cookies shared among 15 children. If each child receives the same amount of pizza, how much will each child get?
Answers
Help pls!! Which would not be an enlargement or reduction of the letter below?

Answers
Answer:
I would think J because they gained the same amount
Which side lengths form a right triangle?

Answers
Answer:
\(\text{A. }3, \sqrt{27}, 6,\\\text{B. }8, 15, 17,\\\text{C. }5, 5, \sqrt{50}\)
Step-by-step explanation:
All right triangles must follow the Pythagorean Theorem \(a^2+b^2=c^2\) where \(c\) is the hypotenuse of the triangle.
Verify:
\(3^2+\sqrt{27}^2=6^2\checkmark,\\8^2+15^2=17^2\checkmark,\\5^2+5^2=\sqrt{50}^2\checkmark\)
Answer:
Option : A, B, C
Step-by-step explanation:
To make sure the lengths form sides of a triangle we use Pythagoras theorem:
Square of length of larger side = Sum of square of smaller sides.
\((A) 3, \sqrt{27}, 6: => 6^2 = 3^2 + (\sqrt{27})^2\)
\(36 = 9 + 27\\36 = 36\\Satisfies \ Pythagoras \ Theorem\)
\((B) 8, 15, 17 :=> 17^2 = 15^2 + 8^2\)
\(289 = 225 + 64 \\289 = 289 \\Satisfies \ the \ condition\)
\((C) 5, 5 , \sqrt{50} :=> (\sqrt{50})^2 = 5^2 +5^2\\\)
\(50 = 25 + 25 \\50 = 50\\Satisfies \ the \ condition\)
Can y’all solve this please

Answers
Answer:
a. the coordinates of g = 1 and -5
explanation
x-1=0 OR x+5=0
collect like terms
x=1. OR x=-5
What is the best way to solve this?

Answers
Answer:
20+20+20=60
20+5+5=30
5-2=3
1+(20*5)=100+1=101
Step-by-step explanation:
Hope it helps :)
Answer:
you do order of operations
Step-by-step explanation:
2. bn = 5.4-n
3. by = 4.5"
Answers
Answer:
what is the question?
Step-by-step explanation:
T/F if an > 0 and lim n→[infinity] an + 1 an < 1, then lim n→[infinity] an = 0.
Answers
The expression aₙ > 0 and lim n → [∞] aₙ + 1 is true.
The term expression in math is defined as a sentence with a minimum of two numbers or variables and at least one math operation.
Here we have given that if an > 0 and lim n→[infinity] an + 1 an < 1, then lim n→[infinity] an = 0.
And we need to check whether the given statement is true or not.
While we looking into the given question, we have identified the following expression,
=> lim n → [∞] aₙ + 1
Here we have also know that the value of aₙ > 0.
When we equate the given expression with zero, we have get the following expression,
=> lim n → [∞] aₙ + 1 = 0
=> lim n → [∞] aₙ = -1
Here we have given the condition that, aₙ >0, so
=> lim n → [∞] aₙ = 0
Therefore, the expression is zero.
To know more about Expression here.
https://brainly.com/question/14083225
#SPJ4
When do we use n, p and q? When we are testing a proportion, a
mean (average), or both?
Explain.
Answers
When testing a proportion, we use p and q to represent the proportion of success and failure, respectively.
For example, if we are testing the proportion of students who passed a test, we would use p to represent the proportion who passed and q to represent the proportion who did not pass.
When testing a mean (average), we use n to represent the sample size. For example, if we are testing the average height of a sample of individuals, we would use n to represent the number of individuals in the sample.
In some cases, we may use all three terms when testing both a proportion and a mean. For example, if we are testing the proportion of students who passed a test and the average score of those who passed, we would use p and q to represent the proportion of success and failure, and n to represent the sample size of those who passed. We would also use the mean to represent the average score of those who passed.
To know more about hypothesis testing visit:
https://brainly.com/question/28920252
#SPJ11
6 16 Next → Pretest: Scientific Notation Drag the tiles to the correct boxes to complete the pairs.. Particle Mass (grams) proton 1.6726 × 10-24 The table gives the masses of the three fundamental particles of an atom. Match each combination of particles with its total mass. Round E factors to four decimal places. 10-24 neutron 1.6749 × electron 9.108 × 10-28 two protons and one neutron one electron, one proton, and one neutron Mass 0-24 grams two electrons and one proton one proton and two neutrons Submit Test Particles F
Answers
We can drag the particles in mass/grams measurement to the corresponding descriptions as follows:
1. 1.6744 × 10⁻²⁴: Two electrons and 0ne proton
2. 5.021 × 10⁻²⁴: Two protons and one neutron
3. 5.0224 × 10⁻²⁴: One proton and two neutrons
4. 3.3484 × 10⁻²⁴: One electron, one proton, and one neutron
How to match the particlesTo match the measurements to the descriptions first note that one neutron is 1.6749 × 10⁻²⁴. One proton is equal to 1.6726 × 10⁻²⁴ and one electron is equal to 9.108 × 10⁻²⁸.
To obtain the right combinations, we have to add up the particles to arrive at the constituents. So, for the figure;
1.6744 × 10⁻²⁴, we would
Add 2 electrons and one proton
= 2(9.108 × 10⁻²⁸) + 1.6726 × 10⁻²⁴
= 1.6744 × 10⁻²⁴
The same applies to the other combinations.
Learn more about electrons and protons here:
https://brainly.com/question/1481324
#SPJ1
"Three hundred seventy-two feet below sea level" would be expressed by the integer
Answers
Answer:
-372
Step-by-step explanation:
"Three hundred seventy-two feet" in words can be translated into 372 ft in numbers.
Sea level is often referred to as the integer 0. Altitudes above sea level are referred to as positive numbers, or numbers greater than 0 while altitudes below sea level are referred to as negative numbers, or numbers less than 0.
Because we're talking about 372 ft below sea level, this expresses the integer -372.
I hope this helps!