Calculate the consumers' surplus (in dollars) at the indicated unit price p for the demand equation.
p = 8 − 2q^1⁄3; p = 4
Answers
The consumer surplus at the indicated unit price p = 4 for the demand equation p = 8 - 2\(q^{1/3}\) is: $16.
To calculate the consumer surplus at the indicated unit price p for the demand equation p = 8 - 2\(q^{1/3}\) with p = 4, follow these steps:
1. Substitute the given price (p = 4) into the demand equation:
4 = 8 - 2\(q^{1/3}\)
2. Solve for q:
2\(q^{1/3}\) = 8 - 4
\(q^{1/3}\) = 2\(q^{1/3}\)
q = \(2^3\)
q = 8
3. Now, calculate the consumer surplus using the formula: Consumer Surplus = (1/2) × Base × Height
- The base is the quantity (q) at the given price, which is 8.
- The height is the difference between the maximum price the consumers are willing to pay (8) and the actual price they pay (4).
4. Calculate the consumer surplus:
Consumer Surplus = (1/2) × 8 × (8 - 4)
Consumer Surplus = 4 × 4
Consumer Surplus = 16
Thus, the consumer surplus at the indicated unit price p = 4 for the demand equation p = 8 - 2\(q^{1/3}\) is $16.
To know more about "Consumer surplus" refer here:
https://brainly.com/question/15416023#
#SPJ11
Related Questions
Which of the following is most likely the next step in the series?

Answers
Answer:
A
Step-by-step explanation:
Two vertical then probably two horizontal
Answer:
C
Step-by-step explaintion:
write a linear equation for f(5)=7 and f(-2)=0
Answers
Answer:
y = x + 2
Step-by-step explanation:
We start by writing the coordinates pair
(x, f(x))
So we have;
(5,7) and (-2,0)
We start by getting the slope;
m = y2-y1/x2-x1
m = 0-7/-2-5 = -7/-7 = 1
The equation of a linear equation has the general form;
y = mx + c
m is the slope and c is the y-intercept
y = x + c
to get the value of c, we make a simple substitution
we can use the x and y values of any point
7 = 5 + c
c = 7-5
c = 2
So the equation is;
y = x + 2
-x^2 +x+6=0 (Please solve by completing the square, and show steps)
Answers
The solution to the equation using the completing the square are 2 and -3
Quadratic equationThese are equation that has a leading degree of 2. Given the equation below
-x^2 +x+6=0
This can also be written as
x^2-x-6 = 0
Complete the square
x^2-x = 6
x^2-x+ (1/2)^2 = 6 + (1/2)^2
(x-1/2)^2 = 6 + 1/4
(x+1/2)^2 = 25/4
x+1/2 = ±√25/4
x = 5/2 -1/2 or -5/2-1/2
x = 4/2 or -6/2
x = 2 and -3
Hence the solution to the equation using the completing the square are 2 and -3
Learn more on completing the square here: https://brainly.com/question/13981588
#SPJ1
a sketch of y = x^2 + cx + d is shown the turning point is (2,3) work out the values of c and d
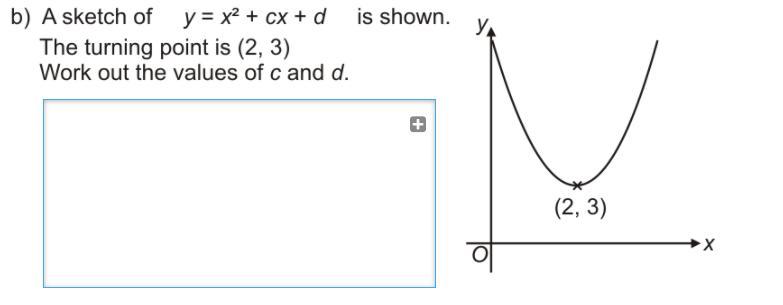
Answers
Answer:
c= - 4, d = 7Step-by-step explanation:
Given function:
y = x² + cx + dThe vertex is (2, 3)
We know the vertex form:
y = (x - h)² + k, where (h, k) is vertexSubstitute coordinates to get:
y = (x - 2)² + 3 = x² - 4x + 4 + 3 = x² - 4x + 7Compare with given to find out:
c = - 4, d = 7Ariana has $12.00 worth of nickels and dimes. she has a total of 149 coins (nickels and dimes). determine the number of nickels and the number of dimes that ariana has. ariana has dimes and nickels. (be sure to label the numbers as # of dimes and # of nickels.)#
Answers
The number of nickels and dimes that Ariana has are 58 and 91
Linear Equation:
The polynomial equation with 1 degree representing an unknown quantity is known as a Linear equation. Here to represent the unknown quantity we will use variables like x, y, z .... etc.
From the given problem,
The amount that Ariana = $12.00
As we know 1 dollar = 100 cents
⇒ $12.00 = 12 × 100 = 1200 cents
Total number of nickels and dimes = 149
Since we don't know the number of nickels and dimes we will represent them with variables x and y respectively.
The amount of x nickels coins
= x × 5 cents = 5x cents [ ∵ nickels = 5 cents ]
The amount of y dimes coins
= y × 10 cents = 10y cents [ ∵ dimes = 10 cents ]
From the above calculations the equation that can be formed
Total amount that Ariana is 5x + 10y = 1200 cents
=> x + 2y = 240 ----- Equation (1)
Total number of coins is x + y = 149 ----- Equation (2)
Now solve (1) and (2) to find the number of each coin
Do (1) - (2)
=> x + 2y - [ x + y ] = 240 - 149
=> x + 2y - x - y = 91
=> y = 91
Substitute y = 91 in Equation (2)
(2) => x + 91 = 149
=> x = 58
The number of nickels and dimes that Ariana has are 58 and 91
Learn more about Linear Equation problems at
https://brainly.com/question/16141830
#SPJ4
Select ALL the side lengths that make a right triangle. *
3,6,7
1,2,4
3,4,5
5,9,10

Answers
3,4,5 is correct
as we know that ,
3² + 4² = 5²
9 + 16 = 5²
25 = 25
hence . 3,4,5 is correct
Answer:
I'm pretty sure it's 3,4,5 but I'm not sure (is it in cm,mm etc?)
A bike rental costs $8 per hour. Desiree has a coupon for 2 free hours. To find how many hours she can rent with $40, Desiree sets up the equation 8(x – 2) = 40, where x is the number of hours.
Answers
Answer:
40
Step-by-step explanation:
8x = 56
8x + 16 = 40
x = 3
8x = 24
x = 7
8x – 16 = 40
8(x – 2) = 40
find the derivative of the following function, with a positive index (differentiation)
pls help there’s a picture

Answers
Answer:
2nd option
Step-by-step explanation:
Using the power rule
\(\frac{d}{dx}\) (a\(x^{n}\) ) = na\(x^{n-1}\)
Given
f(x) = \(\frac{3}{2\sqrt[3]{x} }\) = \(\frac{3}{2x^{\frac{1}{3} } }\) = \(\frac{3}{2}\) \(x^{-\frac{1}{3} }\) , then
f'(x) = - \(\frac{1}{3}\) × \(\frac{3}{2}\) \(x^{-\frac{4}{3} }\)
= - \(\frac{1}{2}\) × \(\frac{1}{x^{\frac{4}{3} } }\)
= - \(\frac{1}{2x^{\frac{4}{3} } }\) = - \(\frac{1}{2\sqrt[3]{x^4} }\) [ Note there should be a leading negative ]
A Ferris wheel is 15 meters in diameter and boarded from a platform that is 1 meters above the ground. The six o'clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. How many minutes of the ride are spent higher than 15 meters above the ground?
Answers
Answer:
The number of minutes of the ride that are spent higher than 15 meters above the ground is 18 minutes.
Step-by-step explanation:
We will use the sin function for the height of the Ferris wheel.
\(y=A\ sin(B(x+C))+D\)
A = amplitude
C = phase shift
D = Vertical shift
2π/B = period
From the provided information:
A = 15/2 = 7.5 m
\(Period=2\\\\\frac{2\pi}{B}=2\\\\B=\pi\)
Compute the Vertical shift as follows:
D = A + Distance of wheel from ground
= 7.5 + 1
= 8.5
The equation of height is:
\(h(t)=7.5\cdot sin(\pi (t+C))+8.5\)
Now at t = 0 the height is, h (t) = 1 m.
Compute the value of C as follows:
\(h(t)=7.5\cdot sin(\pi (t+C))+8.5\)
\(1=7.5\cdot sin(\pi (0+C))+8.5\\\\-7.5=7.5\cdot sin\ \pi C\\\\sin\ \pi C=-1\\\\\pi C=sin^{-1}(-1)\\\\\pi C=\frac{3\pi}{2}\\\\C=\frac{3}{2}\)
So, the complete equation of height is:
\(h(t)=7.5\cdot sin(\pi (t+\frac{3}{2}))+8.5\)
Compute the number of minutes of the ride that are spent higher than 15 meters above the ground as follows:
h (t) ≥ 15
\(h(t)=15\\\\7.5\cdot sin(\pi (t+\frac{3}{2}))+8.5=15\\\\7.5\cdot sin(\pi (t+\frac{3}{2}))=6.5\\\\sin(\pi (t+\frac{3}{2}))=\frac{6.5}{7.5}\\\\(\pi (t+\frac{3}{2}))=sin^{-1}[\frac{13}{15}]\\\\\pi (t+\frac{3}{2})=60.074\\\\t+\frac{3}{2}=19.122\\\\t=17.622\\\\t\approx 18\)
Thus, the number of minutes of the ride that are spent higher than 15 meters above the ground is 18 minutes.
a school librarian wanted to estimate the proportion of students in the school who had read a certain book. the librarian sampled 50 students from the senior english classes, and 35 of the students in the sample had read the book. have the conditions for creating a confidence interval for the population proportion been met? responses yes, because the sample was selected at random. yes, because the sample was selected at random. yes, because sampling distributions of proportions are modeled with the normal model. yes, because sampling distributions of proportions are modeled with the normal model. yes, because the sample is large enough to satisfy the normality conditions. yes, because the sample is large enough to satisfy the normality conditions. no, because the sample is not large enough to satisfy the normality conditions. no, because the sample is not large enough to satisfy the normality conditions. no, because the sample was not selected using a random method.
Answers
The normality assumption is valid.
The librarian can proceed to create a confidence interval for the population proportion of students in the school who have read the book.
The school librarian has a goal of estimating the proportion of students in the school who have read a particular book. The librarian sampled 50 students from the senior English classes, and out of those 50 students, 35 of them had read the book.
The question at hand is whether the conditions for creating a confidence interval for the population proportion have been satisfied.
Firstly, it is essential to establish that the sample was selected at random.
According to the question, this has been done.
It is a crucial condition because it helps to avoid bias in the sample.
If the sample had not been selected at random, there would be a risk of under- or over-representing certain groups, leading to an inaccurate estimation of the proportion of students who have read the book.
Secondly, sampling distributions of proportions are modeled with the normal model.
This condition has been met because the sample size (50 students) is greater than or equal to 30.
When the sample size is this large, the sampling distribution of proportions can be approximated to the normal distribution.
The normality assumption is valid when the sample size is large enough to satisfy the rule of thumb of np≥10 and nq≥10.
Thus, both conditions for creating a confidence interval for the population proportion have been met.
The sample was selected at random, and the sample size is greater than or equal to 30.
For similar question on assumption.
https://brainly.com/question/29672185
#SPJ11
Tanisha and her children went into a restaurant that sells hamburgers for
$7.50 each and drinks for $1.75 each. Tanisha has $70 to spend and must buy
no less than 18 hamburgers and drinks altogether. If a represents the number
of hamburgers purchased and y represents the number of drinks purchased,
write and solve a system of inequalities graphically and determine one
possible solution.
Answers

CALCULATE PR :)
Merry Xmas btw

Answers
Answer:
PR = 7.9
Step-by-step explanation:
By sine rule:
\( \frac{12.5}{ \sin \: 66 \degree} = \frac{PR}{ \sin \: 37 \degree} \\ \\ \frac{12.5}{ 0.9135454576} = \frac{PR}{ 0.6018150232} \\ \\ PR = \frac{12 \times 0.6018150232}{0.9135454576} \\ \\ PR = \frac{12 \times 0.6018150232}{0.9135454576} \\ \\PR = \frac{7.22178028}{0.9135454576} \\ \\ PR = 7.90522269 \\ \\ PR \approx \: 7.9\)
5.
Which of the following equations describes the graph?

Answers
Step-by-step explanation:
I've been a substitute for a few day for College students so the answer is y equal s x2-5x+2
pls help meee 100 points
Explain why this comparison is either reasonable
3.4< 3.36
WHAT DO I PUT IN
100 points if you help mee
Answers
Answer: The comparison "3.4 < 3.36" is reasonable because 3.36 is greater than 3.4.
The decimal point separates the whole number part of a number from the fractional part. In this case, 3.36 has a greater whole number part (3) than 3.4, and both have the same decimal part (0.36). So, 3.36 is greater than 3.4.
Therefore, the statement "3.4 < 3.36" is a true and reasonable comparison.
Step-by-step explanation:
Carlisle Transport had $4,520 cash at the beginning of the period. During the period, the firm collected $1,654 in receivables, paid $1,961 to supplier, had credit sales of $6,916, and incurred cash expenses of $500. What was the cash balance at the end of the period?
Answers
To calculate the cash balance at the end of the period, we need to consider the cash inflows and outflows.
Starting cash balance: $4,520
Cash inflows: $1,654 (receivables collected)
Cash outflows: $1,961 (payments to suppliers) + $500 (cash expenses)
Total cash inflows: $1,654
Total cash outflows: $1,961 + $500 = $2,461
To calculate the cash balance at the end of the period, we subtract the total cash outflows from the starting cash balance and add the total cash inflows:
Cash balance at the end of the period = Starting cash balance + Total cash inflows - Total cash outflows
Cash balance at the end of the period = $4,520 + $1,654 - $2,461
Cash balance at the end of the period = $4,520 - $807
Cash balance at the end of the period = $3,713
Therefore, the cash balance at the end of the period is $3,713.
To learn more about cash : brainly.com/question/31754110
#SPJ11
Can somebody help me please

Answers
Answer:
y=-5/2x+(Any number)
Step-by-step explanation:
First, find the slope of that line
3+2=5
-5+7=2
5/2 is the slope
Perpendicular lines have the slope that is opposite and a fliped sign
This means that the slope should be -2/5
The equation of the line would be y=-5/2x+(Any number)
Last year, Aldo opened an investment account with . At the end of the year, the amount in the account had decreased by . How much is this decrease in dollars? How much money was in his account at the end of last year?

Answers
That leaves $6019 in the account by subtraction
What is the area of the shape?

Answers
Answer: 21 units²
Step-by-step explanation:
Since there is a pair of parallel sides, this figures is a trapezoid. The formula for the area of a trapezoid is \(\frac{1}{2}(a+b)h\), where a and b are the parallel sides and h is the height.
Here, a and b are 5 and 9, while 3 is the height. Let's put all 3 values into the formula.
\(A=\frac{1}{2}(5+9)*3\)
\(A=\frac{1}{2}(14)*3\) [Adding in the parentheses]
\(A=7*3\) [Multiplying one-half by 14]
\(A=21\) [Multiplying 7 and 3]
The area is 21 units².
What is the value of v?

Answers
Answer:
70 degrees.
Step-by-step explanation:
They are vertical angles, and vertical angles are always congruent.
A study of homeowners in the 5th congressional district in Maryland found that their annual household incomes are normally distributed with a mean of $41,182 and a standard deviation of $11,990 (based on data from Nielsen Media Research). If an advertising campaign is to be targeted at those whose household incomes are in the top 20%, find the minimum income level for this target group.
Answers
Answer:
The minimum income level for this target group is of $51,253.6.
Step-by-step explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of $41,182 and a standard deviation of $11,990
This means that \(\mu = 41182, \sigma = 11990\)
Find the minimum income level for this target group.
The 100 - 20 = 80th percentile, which is X when Z has a p-value of 0.8, so X when Z = 0.84.
\(Z = \frac{X - \mu}{\sigma}\)
\(0.84 = \frac{X - 41182}{11990}\)
\(X - 41182 = 0.84*11990\)
\(X = 51253.6\)
The minimum income level for this target group is of $51,253.6.
Mike tabulated the following values for heights in inches of seven of his friends: 65, 71, 74, 61, 66, 70, and 72. The sample standard deviation is 4.577.
Select the 95% confidence interval for Mike's set of data.
Answers
the 95% confidence interval for Mike's set of data is (65.89, 70.97). This means we can be 95% confident that the true population mean falls within this interval.
To find the 95% confidence interval for Mike's set of data, we first need to calculate the sample mean and the standard error of the mean:
Sample mean = (65 + 71 + 74 + 61 + 66 + 70 + 72) / 7 = 68.43
Standard error of the mean = sample standard deviation / sqrt(sample size) = 4.577 / sqrt(7) = 1.732
Next, we can use the formula for the confidence interval:
Confidence interval = sample mean ± (critical value) × (standard error of the mean)
The critical value for a 95% confidence interval with 6 degrees of freedom (n-1) is 2.015.
Plugging in the values, we get:
Confidence interval = 68.43 ± 2.015 × 1.732
Confidence interval = (65.89, 70.97)
what is mean?
In mathematics, the mean is a measure of central tendency of a set of numerical values. It is commonly known as the average, which is obtained by summing up all the values in a data set and dividing by the total number of values. The mean provides an overall idea of the "typical" value in a data set, and is widely used in statistics and data analysis.
To learn more about mean visit:
brainly.com/question/30112112
#SPJ11
solve for x geometry

Answers
Answer:
Step-by-step explanation:
Take the natural logarithm of both sides of the equation to remove the variable from the exponent.
ln
(
6
x
)
=
ln
(
66
)
Expand
ln
(
6
x
)
by moving
x
outside the logarithm.
x
ln
(
6
)
=
ln
(
66
)
Divide each term by
ln
(
6
)
and simplify.
Tap for more steps...
x
=
ln
(
66
)
ln
(
6
)
The result can be shown in multiple forms.
Exact Form:
x
=
ln
(
66
)
ln
(
6
)
Decimal Form:
x
=
2.33829083
…
Answer:
X=19
Step-by-step explanation:
A full line must be 180 degrees and you already know that part of the line is 66 degrees. You do 180 minus 66 which gives you 114. That is the other unknown angle but it is asking for x, not the angle. You do 114 divided by 6 to get 19. Therefore, x=19.
Work out the median of these numbers:
-12, 6, 7, 12, -6, 1

Answers
Answer:
(-12+6+7+12-6+1)÷ 6
=8÷6
=1.3333
lim sin(pi/3+h) - sin(pi/3)/ h as h approaches 0 is
A. 0
B. 1/2
C. 1
D. Square root of 3/2
E. Nonexistent
Answers
lim sin(pi/3+h) - sin(pi/3)/ h as h approaches 0 is Non existent. The correct answer is option e.
To evaluate the limit, we can use the formula for the derivative of sin(x), which is:
lim f(x+h) - f(x) / h as h approaches 0 = f'(x)
where f(x) = sin(x).
So, in this case, we have:
lim sin(pi/3+h) - sin(pi/3) / h as h approaches 0
which can be rewritten as:
lim [sin(pi/3+h) - sin(pi/3)] / h as h approaches 0
Using the identity for the difference of two sines, we can simplify this expression to:
lim [2cos(2pi/6+h/2)sin(h/2)] / h as h approaches 0
Now, we can cancel out the factor of sin(h/2) in the numerator and denominator, and we are left with:
lim 2cos(2pi/6+h/2) / h as h approaches 0
We can evaluate the limit using direct substitution, and we get:
2cos(pi/3) / 0
Since the denominator is 0, the limit does not exist. Therefore, the answer is option E: Nonexistent.
To know more about derivative refer to-
https://brainly.com/question/30365299
#SPJ11
The diagram shows a rectangle PQRS.
PQ = 14 cm and QR = 9 cm.
The point A lies on PS so that PA = 5 cm.
The point Blies on SR so that BR = 8 cm.

Answers
Answer:
a) The area of the triangle AQB is 43 square centimeters.
b) The length of the line segment AQ is approximately 14.866 centimeters.
Step-by-step explanation:
a) The procedure consist in subtracting the areas of triangles APQ, ASB and BRQ of the area the rectangle, that is to say:
\(A = (9\,cm)\cdot (14\,cm) - \frac{1}{2}\cdot (5\,cm)\cdot (14\,cm) - \frac{1}{2}\cdot (8\,cm)\cdot (9\,cm) -\frac{1}{2}\cdot (4\,cm) \cdot (6\,cm)\)
\(A = 43\,cm^{2}\)
The area of the triangle AQB is 43 square centimeters.
b) The length of the line segment AQ is determined by Pythagorean Theorem:
\(AQ = \sqrt{AP^{2}+PQ^{2}}\) (1)
\(AQ = \sqrt{(5\,cm)^{2}+(14\,cm)^{2}}\)
\(AQ \approx 14.866\,cm\)
The length of the line segment AQ is approximately 14.866 centimeters.
The graphus buscou have the same shape. What is the equation of the grand
do
2
10
A.g(x)= x^2-3
B.g (x) = (x+3)^2
c. g(x) = x^2 + 3
D. g(x) = (x-3)^2

Answers
Answer:
C. g(x) = x^2 + 3
Step-by-step explanation:
A data-entry clerk spends $86 per week for food. This is 20% of his weekly income. What is the weekly income? Show work please :
Answers
Answer:
$430
Step-by-step explanation:
Let the weekly income be x
Money spent on food= $86
% of weekly income spent on food = 20
20% of weekly income in terms = 20/100 * x = x/5
This, income is equal to $86 as given
thus,
x/5 = 86
x = 86*5 = 430
Thus, weekly income is $430.
please help me answer this question asap

Answers
Answer:
It's quite easy
Step-by-step explanation:
people less than 30 years = frequency of people 0 to 15 + 15 to 30 = 8+15 =23
Therefore there are 23 people less than 30 years old.
pls mark me as brainliest pls.
find two unit vectors that make an angle of 60° with v = 8, 6
Answers
The two unit vectors are (2/5 +√5/10, 3/10 + 2√5/15) and (2/5 -√5/10, 3/10 - 2√5/15).
Given that, Angle = 60°, v = 8, 6
Consider unit vector a = (x, y)
x² + y² = 1 …. (1)
Now apply the dot product of unit vector with v
a.v = |a||v|cos Ø
a.v = √ (x² + y²) √ (8² + 6²) cos 60º
8x + 6y = 1 × 10 × ½
So we get,
8x + 6y = 5 …. (2)
y = (5 - 8x) / 6
Substituting the value of y in equation (1)
x² + y² = 1
x² + [(5 - 8x)/6]² = 1
x² + 25/36 + 16x²/9 - 20x/9 = 1
25x²/9 - 20x/9 = 11/36
So we get,
4 × (25x² - 20x) = 11
100x² - 80x = 11
100x² - 80x - 11 = 0
Now solve the quadratic equation,
x = { 2/5 ± √5/10}
Substituting the value of x in equation (2)
y = 3/10 ± 2√5/15
Therefore, the two unit vectors are (2/5 +√5/10, 3/10 + 2√5/15) and (2/5 -√5/10, 3/10 - 2√5/15).
Learn more about unit vectors click;
https://brainly.com/question/28028700
#SPJ1
the following gives task duration for software project activities. what is the minimum number of days to finish this project? task duration (days) dependencies t1 8 t2 6 t1 t3 10 t1, t2 t4 7 t3 t5 12 t2, t3 t6 15 t4, t5
Answers
Step-by-step explanation:
To calculate the minimum number of days required to finish this project, we need to use the critical path method (CPM), which involves identifying the longest sequence of dependent tasks and their durations.
First, we need to draw the network diagram for the project:
```
|---(T1-8)---(T3-10)---|
(T2-6) (T5-12)
| / |
|---(T4-7)---(T6-15)---|
```
Next, we need to calculate the earliest start time (EST), earliest finish time (EFT), latest start time (LST), and latest finish time (LFT) for each task. For the starting task, EST = 0 and EFT = 0.
```
EST EFT LST LFT
T1 (8 days) 0 8 22 30
T2 (6 days) 0 6 6 12
T3 (10 days) 8 18 22 32
T4 (7 days) 18 25 25 32
T5 (12 days) 18 30 32 44
T6 (15 days) 32 47 32 47
```
The critical path is the longest sequence of dependent tasks that have no slack (i.e., the difference between LST and EST, or LFT and EFT, is zero). In this case, the critical path is T1-T3-T5-T6.
Therefore, the minimum number of days to finish this project is the sum of the durations of tasks on the critical path:
8 + 10 + 12 + 15 = 45 days
Therefore, the minimum number of days required to finish this project is 45 days.