The Ramirez family has a circular garden with a diameter of 22 ft. They cover the garden with mulch. The cost of mulch is $1.25 per square foot. To the nearest dollar, how much will it cost to cover the garden in mulch? Show your work
Answers
Answer:
$475
Step-by-step explanation:
r = 11 ft
Area of garden: πr² = π (11 ft)² = 379.94 ft²Cost: 379.94 ft² x $1.25/ft² = $474.93Related Questions
Why
is 30% of 40
and 40% of 30 the
same?
Answers
Answer:
no it's different 30% would be 12 and 40% would be 16 if it was going into 30 now mark as brainliest
Answer:
In both cases you are really multiplying the same numbers together.
Step-by-step explanation:
30% of 40 would be 30 x 40 x 0.01 = 12
or 0.30 x 40 = 12
40% of 30 would be 40 x 30 x 0.01 = 12
or 30 x 0.40 = 12
> Function g can be thought of as a translated (shifted) version of Y f(x) = x².
Answers
Using translation concepts, function g(x) is given as follows:
g(x) = x² - 3.
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
Researching this problem on the internet, g(x) is a shift down of 3 units of f(x) = x², hence:
g(x) = x² - 3.
More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
Determine if the triangle with the given sides is acute, obtuse, or right.
7, 12, 16
Answers

Like us, mice are warm-blooded creatures. Their bodies must maintain a constant
temperature of 37°C, regardless of the temperature of their environment. Doing so burns
calories. The more severe the temperature difference, the more calories the mouse must
burn to maintain its body temperature. Consulting the research literature, you found the
following model:
C = 0.37219T + 1,560
Where C is the number of calories an idle mouse burns each day and T is the temperature
of its environment in °C. What is the most comfortable temperature for an idle mouse?
(This is the temperature where it burns the least calories per day). How many calories will
it burn each day at that temperature?
Answers
At a temperature of 20°C, the mouse would burn approximately 1,567.44 calories each day.
According to the given model C = 0.37219T + 1,560, where C represents the number of calories an idle mouse burns each day and T represents the temperature of its environment in °C.
To find the most comfortable temperature for an idle mouse, we need to determine the temperature at which the mouse burns the least amount of calories per day.
To find this temperature, we can minimize the equation C = 0.37219T + 1,560. To do so, we take the derivative of C with respect to T and set it equal to zero:
dC/dT = 0.37219 = 0
Solving this equation, we find that the derivative is a constant value, indicating that the function C = 0.37219T + 1,560 is a linear equation with a slope of 0.37219. This means that the mouse burns the least calories at any temperature, as the slope is positive.
Therefore, there is no specific "most comfortable" temperature for an idle mouse in terms of minimizing calorie burn. However, if we consider the range of temperatures mice typically encounter, we can find a temperature where the calorie burn is relatively low.
For example, if we take a temperature of 20°C, we can calculate the calorie burn:
C = 0.37219 * 20 + 1,560
C = 7.4438 + 1,560
C ≈ 1,567.4438 calories per day
Therefore, at a temperature of 20°C, the mouse would burn approximately 1,567.44 calories each day.
For more such questions temperature,click on
https://brainly.com/question/25677592
#SPJ8
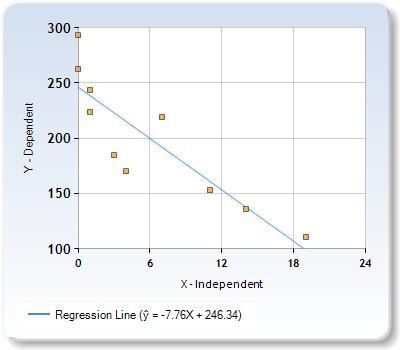
Part Four: Stephen collected data from a travel website. The data included a hotel's distance from Times Square in Manhattan and the cost of a room for one weekend night in August. A table containing these data appears below.
Distance From Times Square
(city blocks) (x) 0 0 1 1 3 4 7 11 14 19
Cost of a Room
($) (y) 293 263 244 224 185 170 219 153 136 111
Write the linear regression equation for this data set. Round all values to the nearest hundredth. State the correlation coefficient for this data set, to the nearest hundredth. Explain what the sign of the correlation coefficient suggests in the context of the problem.
Answers
The equation of the linear regression is \(\^ y = -7.76\^x + 246.34\)
Graphing toolTo determine the line of best fit, we make use of a graphing tool
See attachment for the graph of the line of best fit
The equationFrom the graphing tool, we have the following calculation summary
Sum of X = 60 Sum of Y = 1998 Mean X = 6 Mean Y = 199.8 Sum of squares (SSX) = 394 Sum of products (SP) = -3056The regression Equation is then represented as:
\(\^y = b\^x + a\)
Where:
\(b = \frac{SP}{SSX}\) and \(a = \bar y - b \times \bar x\)
\(b = -\frac{3056}{394}\)
\(b = -7.76\)
Also, we have:
\(a = \bar y - b \times \bar x\)
\(a= 199.8 - (-7.76 \times 6)\)
\(a = 246.34\)
So, the linear regression equation is:
\(\^ y = -7.76\^x + 246.34\)
Read more about linear regression at:
https://brainly.com/question/17844286
Answer:
Step-by-step explanation:
The equation of the linear regression is
Graphing tool
To determine the line of best fit, we make use of a graphing tool
See attachment for the graph of the line of best fit
The equation
From the graphing tool, we have the following calculation summary
Sum of X = 60
Sum of Y = 1998
Mean X = 6
Mean Y = 199.8
Sum of squares (SSX) = 394
Sum of products (SP) = -3056
The regression Equation is then represented as:
Where:
and
Also, we have:
So, the linear regression equation is:
Read more about linear regression at:
brainly.com/question/17844286
The equation of the linear regression is \(\^ y = - 1
NEED HELP NOW!! PLEASE
A baseball diamond is a square with sides of 90 feet. What is the distance, to the nearest tenth of a foot, between home and second base?
Answers
f(x)=x^3+5x+k and x+2 is a factor of f(x), then what is the value of k?
Answers
The value of k is 18.
If x + 2 is a factor of f(x) = x^3 + 5x + k, it means that when x = -2, the expression f(x) becomes zero.
Substituting x = -2 into f(x), we have:
f(-2) = (-2)³ + 5(-2) + k
= -8 - 10 + k
= -18 + k
Since f(-2) should equal zero, we have:
-18 + k = 0
k = 18
Therefore, the value of k is 18.
Learn more about Factor here:
https://brainly.com/question/30612677
#SPJ1
what is 5 1/2 + 2 1/7 pleas help i cant figure it out
Answers
Answer:
\(\frac{107}{14}\) or \(7\frac{9}{14}\)
Step-by-step explanation:
\(5 \frac{1}{2} +2\frac{1}{7}\)
\(5 \frac{1}{2} +2\frac{1}{7} =\frac{11}{2} +\frac{15}{7}\)
\(\frac{11}{2} +\frac{15}{7}\)
\(\frac{11}{2} +\frac{15}{7}=\frac{77+30}{14} =\frac{107}{14}\)
\(\frac{107}{14} =7\frac{9}{14}\)
Hope this helps!
Solve x2-x-5/2 = 0 using the quadratic formula.
the answer choices are in the picture

Answers
Answer:
Exact Form: x =( 1 ± √ 11) /2
It's the first one.
Step-by-step explanation:
Solve the equation for x by finding a , b , and c of the quadratic then applying the quadratic formula.
Solve for p.
p − 4
2
= 3
Answers
The value of p in the expression is 45
What is additive inverse?Additive inverse simply means changing the sign of the number and adding it to the original number to get an answer equal to 0.
For example a+5 = 2 , by solving this we add the additive inverse of 5 to both sides. The additive inverse of 5 is -5
this means,
a+5-5 = 2-5
a = 2-5
a = -3
Similarly, p-42 = 3 is solved in the same way. we add the additive inverse of -42 which is +42 to both sides,
p-42+42 = 3+42
p = 3+42
p = 45
therefore the value of p is 45
learn more about additive inverse from
https://brainly.com/question/1548537
#SPJ1
A number N gives remainder 0 when divided by 8, it gives remainder 0, when divided by 7 and it is an even multiple of 5. Find the least positive number N with this property
Answers
The least positive number with this property is given as follows:
N = 280.
How to obtain the number?A number N gives remainder 0 when divided by 8, it gives remainder 0, when divided by 7 and it is an even multiple of 5, hence the number is multiple of these 3 numbers.
Before obtaining the number, we must obtain the least common multiple of 8, 7 and 5, factoring them by prime factors as follows:
8 - 7 - 5|2
4 - 7 - 5|2
2 - 7 - 5|2
1 - 7 - 5|5
1 - 7 - 1|7
1 - 1 - 1.
Hence:
lcm(8,7,5) = 2³ x 5 x 7 = 280.
280 is an even multiple of 5, as it is an even number, hence it is the least positive number N with the property in this problem.
More can be learned about the least common multiple at https://brainly.com/question/10749076
#SPJ1
The Language Arts department conducts a study to see if the number of books a student reads per month affects the score on the SAT Verbal Test. Here is the data that the Language Arts department collected for 8 students. Create the scatter plot for this data set. What is the equation of the line of best fit?
Answers
A scatter plot visually represents the relationship between two variables. It shows a positive correlation between the number of books read per month and SAT Verbal Test scores, with the equation y = 6.4828x + 520.6962.
A scatter plot is a graphical representation of a set of data that allows the observer to observe the relationship between two variables. It is used to graphically display how one variable is affected by the other. It is a chart of data points plotted on a two-dimensional graph with one variable represented on the X-axis and the other variable on the Y-axis.
Scatter Plot of the Data: From the data provided by the Language Arts department, we can create the scatter plot as shown below:
Equation of the line of best fit: The line of best fit is a straight line that is used to model the relationship between the two variables. It is determined by minimizing the sum of the squares of the differences between the observed values and the predicted values.
From the scatter plot, we can see that there is a positive correlation between the number of books read per month and the score on the SAT Verbal Test. This suggests that the more books a student reads per month, the higher their score on the SAT Verbal Test.
The equation of the line of best fit for the given data set is y = 6.4828x + 520.6962. Here, y represents the score on the SAT Verbal Test and x represents the number of books read per month.
To find the equation of the line of best fit, we can use a regression analysis tool such as Excel. The regression analysis will give us the values of the slope and intercept of the line of best fit, which we can use to write the equation of the line.
For more questions on a scatter plot
https://brainly.com/question/30756481
#SPJ8
On October 12, 2020, the number of new cases of Covid 19 in Milwaukee was 235. On Oct. 22, 2020, the number of new cases in Milwaukee was 395.
a. Create an exponential model for new cases in terms of days.
b. Based on your model, what would be the number of new cases on Oct. 31, 2020?
c. The actual number of new cases on Oct. 31, 2020, was 1043. How well does this fit your model?
Answers
a. To create an exponential model for new cases in terms of days, we can use the formula: y = a * b ^ x, where y is the number of new cases, x is the number of days since the first observation, and a and b are constants that we need to determine. Using the two data points given, we can set up a system of equations:
235 = a * b ^ 0
395 = a * b ^ 10
Solving for a and b, we get:
a = 235
b = (395/235)^(1/10) = 1.067
Therefore, the exponential model for new cases in Milwaukee is:
y = 235 * 1.067 ^ x
b. To find the number of new cases on Oct. 31, 2020, we need to plug in x = 19 (since Oct. 31 is 19 days after Oct. 12) into the model:
y = 235 * 1.067 ^ 19 = 1018.5
Therefore, based on the exponential model, we would expect around 1019 new cases on Oct. 31, 2020.
c. The actual number of new cases on Oct. 31, 2020, was 1043. This is higher than the predicted value of 1019, but not by a huge margin. Overall, the model seems to fit the data reasonably well, especially considering that there are many factors that can affect the number of new cases in a given area, and that the model is based on only two data points. However, it is worth noting that the exponential model assumes that the growth rate of new cases remains constant over time, which may not be a realistic assumption in the long run.
The median weekly income for a student who drops out of high school is 451. Someone with a bachelor's degree from college earns 1053 in that same week. Calculate each person's yearly income and then the difference between them.
Answers
The difference between their yearly incomes is $31,304.
To calculate each person's yearly income, we need to multiply their weekly income by the number of weeks in a year. Assuming there are 52 weeks in a year, the yearly income can be calculated as follows:
For the student who drops out of high school:
Yearly Income = Weekly Income x Number of Weeks
= 451 x 52
= 23,452
For someone with a bachelor's degree:
Yearly Income = Weekly Income x Number of Weeks
= 1053 x 52
= 54,756
The difference between their yearly incomes can be found by subtracting the student's yearly income from the bachelor's degree holder's yearly income:
Difference = Bachelor's Yearly Income - Student's Yearly Income
= 54,756 - 23,452
= 31,304
Therefore, the difference between their yearly incomes is $31,304.
It is important to note that these calculations are based on the given information and assumptions. The actual yearly incomes may vary depending on factors such as work hours, additional income sources, deductions, and other financial considerations.
Additionally, it is worth considering that educational attainment is just one factor that can influence income, and there are other variables such as experience, job type, and market conditions that may also impact individuals' earnings.
For more such answers on incomes
https://brainly.com/question/28414951
#SPJ8
Based on the median of the samples, what is a reasonable estimate of the number of students that bike to school? Round to the nearest whole number.
PLEASE ANSWER!!!

Answers
The number of students that bike to school is 18
How to determine the valueThe median is described as the middle number of a set of data when the values are arranged in an ascending order from the least to the greatest.
We should also know that the median is one of the measures of central tendency.
From the information given, we have that the data set representing the number of students is;
10, 11, 12 , 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25
Then, we have that the median number is;
Median = 17 + 18/2
add the values
Median = 35/2
Divide the values
Median = 18 students
Learn more about median at: https://brainly.com/question/26177250
#SPJ1
5.
Coach Smith has three skipping ropes.
The blue rope is 24 feet long and it is 4 times as long as the red rope.
The red rope and green rope are of equal length.
How long is the green rope?
Answers
Answer:
6 feet
Step-by-step explanation:
we'll say the length of blue is B, the length of red is R and the length of green is G. we know B = 24
R multiplied by 4 = B
so R is 6
we also know G = R
so G, or the green rope is 6 feet long
Answer:
6
Step-by-step explanation:
The red rope is 24/4 which is 6 because the blue rope is 4 times as long.
The green rope is also 6 because the red and green rope are the same length.
∠aangle, a and \angle b∠bangle, b are complementary angles. \angle a∠aangle, a measures 44^\circ44
∘
44, degrees.
Answers
Answer:
Step-by-step explanation:
if a and b are complementary angles,then a + b =90
44+b=90
∠b=90-44=46°
Answer:
46
Step-by-step explanation:
if a and b are complementary angles,then a + b =90
44+b=90
∠b=90-44=46°
Adam is finding 10 less than 708 mentally. He thinks the tens digit and the hundreds digit will change. He gets 698 for his answer. Is Adam's thinking correct? Explain.
Answers
Answer:
Adam's thinking is not correct.
When subtracting 10 from 708, we need to borrow 1 from the hundreds digit and add it to the tens digit. This will result in a new hundreds digit of 6 and a new tens digit of 9. The ones digit remains the same. Therefore, the correct answer would be 698.
Adam's answer is also 698, but his reasoning is incorrect. He thinks that both the tens and hundreds digits change, which is not the case. In reality, only the tens digit changes while the hundreds digit decreases by 1 due to the borrowing process.
thank me by marking my answer as brainliest!
In a certain chemical, the ratio of zinc to copper is 3 to 19. A jar of the chemical contains 874 grams of copper. How many grams of zinc does it contain?
It contains
grams of Zinc
Answers
Answer:
138 grams of zinc
Step-by-step explanation:
Zinc : copper = 3 : 19
Let amount of zinc = 138 grams
3 : 19 :: x : 874
Product of means = product of extremes
19 * x = 3 * 874
x = \(\frac{3*874}{19}\)
x = 3 * 46
Zinc = 138 grams
\(\underline{\underline{\sf \bigstar \qquad Solution \qquad \: \bigstar}} \\ \)
Copper and Zinc in the ratio = 3:19Weight of copper in chemical = 874 gramsLet weight of copper be 3x and weight of zinc be 19x.
☯ \(\underline{\boldsymbol{According\: to \:the\: Question\:now :}} \\\)
\(:\implies \textsf {Total weight = weight of copper + weight of zinc} \\ \\ \\ \)
\(:\implies \textsf {Total weight = 3x +19x} \\ \\ \\ \)
\(:\implies \underline{ \boxed{ \textsf {Total weight = 22x}}} \\ \\ \\ \)
⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━
\(\dashrightarrow\:\:\textsf{ Weight of chemical = weight of zinc + weight of copper} \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x = 3x + 19x \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x = 3x + 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x - 3x = 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 19x = 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf x = \dfrac{874}{19} \\ \\ \\ \)
\(\dashrightarrow \: \: \underline{\boxed{ \sf x = 46}} \\ \\ \\\)
⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━━━━
\(\bigstar\:\underline{\frak{Finding \: the \: weight \: of \: the \: zinc \: in \: a \: chemical : }}\)
\(\longrightarrow\:\:\sf weight \: of \: zinc = 3x \\ \\ \\ \)
\(\longrightarrow\:\:\sf weight \: of \: zinc = 3 \times 46 \\ \\ \\ \)
\(\longrightarrow\:\: \underline{ \boxed{\sf weight \: of \: zinc =138 \: grams}} \\ \\ \\ \)
\(\therefore\:\underline{\textsf{The chemical contains \textbf{138 grams}} \textsf{ of zinc}}. \\ \)
y= 22 + 187 – 32Vertex form
Answers
The quadratic equation is:
\(y=x^2+18x+32\)then what we need to do is to complete the square for x, we add in both sides of the inequality (18/2)^2=81
\(y+81-32=x^2+2(9)(x)+9^2\)\(y=(x+9)^2-49\)then the vertex will be (-9,-49)
Answer:
y= 22 + 187 – 32 Vertex form
The toasters produced by a company have a normally distributed life span with a mean of 5.8 years and a standard deviation of 0.9 years, what warranty should be provided so that the company is replacing at most 5% of their toasters sold?
Answers
Answer:
A warranty of 4.32 years should be provided.
Step-by-step explanation:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 5.8, \sigma = 0.9\)
What warranty should be provided so that the company is replacing at most 5% of their toasters sold?
The warranty should be the 5th percentile, which is X when Z has a pvalue of 0.05. So it is X when Z = -1.645.
\(Z = \frac{X - \mu}{\sigma}\)
\(-1.645 = \frac{X - 5.8}{0.9}\)
\(X - 5.8 = -1.645*0.9\)
\(X = 4.32\)
A warranty of 4.32 years should be provided.
What are the domain and range of the function f(x)=-x+3-2? domain: -3 -2 domain: -3 -3 range: y<-2 domain: x>-3 range:y>-2
Answers
For given function function f(x)=-x+3-2, the domain is x > -3 and the range is y ≤ 2. So, correct option is D.
The function f(x)=-x+3-2 is a linear function in the form y=mx+b, where m is the slope and b is the y-intercept. In this case, the slope is -1 and the y-intercept is 1. Therefore, the graph of the function is a straight line that intersects the y-axis at (0,1) and has a slope of -1, meaning that it decreases by 1 for every 1 unit increase in x.
The domain of the function is the set of all possible values of x for which the function is defined. Since there are no restrictions on the value of x in the equation f(x)=-x+3-2, the domain is all real numbers, or (-∞, ∞).
The range of the function is the set of all possible values of y that the function can output. In this case, the lowest possible value of y occurs when x approaches positive infinity, and the highest possible value of y occurs when x approaches negative infinity. Therefore, the range is all real numbers less than or equal to 2, or y ≤ 2.
So, the domain is x ∈ (-∞, ∞) and the range is y ≤ 2. Alternatively, the domain can also be expressed as x > -3, since that is the minimum value of x at which the function is defined.
Correct option is D.
To learn more about domain and range click on,
https://brainly.com/question/15136070
#SPJ1
Complete question is:
What are the domain and range of the function f(x)=-x+3-2?
A) domain: -3 -2
B) domain: -3 -3 range: y<-2
C) domain: x>-3 range:y>-2
D) domain : x>-3 range: y ≤ 2
PLEASE HELP!! I keep getting bots or trolls
How can you restrict the domain of the function f(x) = |x + 4| − 2 so the range of the inverse function, f -1(x), is [-4, ∞)?
A.
x ≥ 4
B.
x ≥ -4
C.
x ≥ 0
D.
x < 4
E.
x ≥ -2
Answers
Answer:
a
Step-by-step explanation:
An angle measures 24º more than the measure of its complementary angle. What is the
measure of each angle?
What are the two angles please hurry
Answers
Answer:
33, 57
(not 100% sure this is correct)
Step-by-step explanation:
90= x +(24 +x)
(drag 90, plus the x's and drag the 24)
90 = 2x + 24
(Subtract 24 from 24 and 90 from 24)
66 = 2x
(Divide both by two)
33 = x
(now use x and plus it by 24)
24 + x = 57
PLEASE HELP DONT IGNORE!!

Answers
Answer:
\(m=-\frac{1}{2}\)
Step-by-step explanation:
\(\Delta y=-1,\,\Delta x=2\\\rightarrow \frac{\Delta y}{\Delta x}=\frac{-1}{2}=-\frac{1}{2}\)
\(\Delta\) represents change in both variables, so we calculate the slope this way.
Answer:
m=-1/2
Step-by-step explanation:
Use slope formula: \(m=\frac{y_{2} -y_{1}}{x_{2}-x_{1}}\)

12 m 20 m 16 m 6m 10m x find the length represented by x for each pair of similar triangles
Answers
Answer:
x = 8mStep-by-step explanation:
Let the two triangles be represented as A and B.
Given two triangles with sides 12m 20m 16m and 6m 10m x.
Lengths of sides of triangle A = 12m, 20m, 16m
Lengths of sides of triangle B = 6m, 10m, x
It can be seen that each length of triangle A are twice that of B i.e triangle B dilated by a factor of 1/2.
A = 2B
Considering the 16m length in triangle A and comparing it with the 'x'm length in triangle B, we can get the unknown length x as shown;
16 = 2x
x = 16/2
x = 8m
The sum of the interior angles of a hexagon is equal to the sum of six consecutive integers. What is the measure of the smallest angle of the hexagon?
Answers
What are the important variables in the problem below?
A test is worth 80 points. Multiple-choice questions are worth 2 points, and
short-answer questions are worth 4 points. If the test has 25 questions, how
many multiple-choice questions are there?
OA. p for points, m for multiple choice
OB. s for short answer, t for test
OC. m for multiple choice, s for short answer
OD. t for test, q for questions
Answers
The important variables are the two types of test questions which can be represented as :
m for multiple choice, s for short answerVariables are used to represent unknown values which could be worked out in a mathematical expression or problem.
The variables or unknown in this case are the type of test questions. which are : m for multiple choice, s for short answer
Therefore, the correct option is C. m for multiple choice, s for short answer
Learn more on word problems:https://brainly.com/question/25693822
#SPJ1
This rectangle represents the base of a rectangular prism. The height of the rectangular prism is 56 m.
What is the volume of the rectangular prism?
Responses
A.212 m³
B.525 m³
C.5,600 m³
D.29,400 m³

Answers
Hope this helps:D
In the rectangle, find the length of AD.

Answers
Answer:
required answer is 9 of your question
