Name the subsets that each number belongs to 35 MARK ALL THAT APPLY
REAL
RATIONAL
IRRATIONAL
NATURAL
WHOLE
INTEGER
Answers
Answer:
Real
Rational
Natural
Whole
Step-by-step explanation:
Because I passed all of my math with 100% so i know this is right
Related Questions
Policies Current Attempt in Progress On May 1, 2021, Sheffield Company sells office furniture for $300000 cash. The office furniture originally cost $746800 when purchased on January 1, 2014. Depreciation is recorded by the straight-line method over 10 years with a salvage value of $80200. What gain should be recognized on the sale? (Hint: Use 7.333333 for years used in calculation.) O $44540. O $22220. O $84080. O $42040. Save for Later -/5 = 1 Attempts: 0 of 1 used Submit Answer
Answers
To calculate the gain on the sale of the office furniture, we need to determine the asset's book value and compare it to the sale price.
First, let's calculate the accumulated depreciation on the furniture. The furniture was purchased on January 1, 2014, and the straight-line depreciation method is used over 10 years with a salvage value of $80,200.
Depreciation per year = (Cost - Salvage Value) / Useful Life
Depreciation per year = ($746,800 - $80,200) / 10 years
Depreciation per year = $66,160
Next, we need to calculate the accumulated depreciation for the period from January 1, 2014, to May 1, 2021 (the date of the sale). This is approximately 7.33 years.
Accumulated Depreciation = Depreciation per year × Years
Accumulated Depreciation = $66,160 × 7.33 years
Accumulated Depreciation = $484,444.80
Now, we can calculate the book value of the furniture:
Book Value = Cost - Accumulated Depreciation
Book Value = $746,800 - $484,444.80
Book Value = $262,355.20
Finally, we can calculate the gain on the sale:
Gain on Sale = Sale Price - Book Value
Gain on Sale = $300,000 - $262,355.20
Gain on Sale = $37,644.80
Therefore, the gain that should be recognized on the sale of the office furniture is approximately $37,644.80.
To know more about depreciation, refer here:
https://brainly.com/question/30531944
#SPJ11
The gain that should be recognized on the sale of the office furniture is $84,080.
The gain is calculated by subtracting the equipment's book value from the sale price. This gain will be reported on the company's income statement. Here is how to calculate the gain:First, find the equipment's book value using the straight-line method of depreciation.
Straight-line depreciation is calculated by taking the difference between the equipment's original cost and its salvage value, and then dividing it by the number of years the equipment is used. The annual depreciation expense is then multiplied by the number of years the equipment is used to find the equipment's book value at the end of its useful life.
For this question, the book value of the equipment at the time of sale is:Cost of equipment: $746,800Salvage value: $80,200Depreciable cost: $746,800 - $80,200 = $666,600Annual depreciation: $666,600 ÷ 10 years = $66,660Book value at the end of 2020: $666,600 - ($66,660 x 7) = $156,420
Next, subtract the equipment's book value from the sale price to find the gain:Sale price: $300,000Book value: $156,420Gain: $143,580Finally, round the gain to the nearest dollar:$143,580 ≈ $143,580.00So the gain that should be recognized on the sale of the office furniture is $84,080.
learn more about gain here:
https://brainly.com/question/31218742
#SPJ11
If f(x) = 3x - 1 and g(x) = x + 2, find (f- g)(x).
Answers
Answer:
(f-g)(x) would be 2x-3
Which relationship exhibits a pattern of exponential growth?*A Income is equal to the square of the number of toys sold each monthB The amount saved is equal to the difference in amount of profit and amount spentC The value of an old coin increases by $80 each yearDThe amount in an account results from 10% interest on $1,000 compounded annually for 5 years
Answers
The compound interest formula is :
\(A=P(1+\frac{r}{n})^{nt}\)where A is the amount in the account, P is the principal, r is the interest rate, t is time, and n is the number of times interest is compounded per time 't'. The variables are A and t, that is, P, r, and n are known. Given that t is on the exponent then the relationship represents an exponential growth. Therefore, the correct answer is:
D. The amount in an account results from 10% interest on $1,000 compounded annually for 5 years
The graph below has the same shape as the graph of G(x) = {4, but it isshifted two units to the right. Complete its equation. Enter exponents usingthe caret (-); for example, enter x4 as x^4. Do not include "G(X) =" in youranswer.5.G(X) =

Answers
ANSWER:
\(G(x)=(x-2)^4\)STEP-BY-STEP EXPLANATION:
We have the following function:
\(G(x)=x^4\)In a function, to move it to the right or to the left we must add if we want to move to the left and we must subtract if we want to move to the right.
But we must add or subtract within the exponent, since it moved 2 to the right we must subtract 2 units, just like this:
\(G(x)=(x-2)^4\)The time is 6o'clock. What are the next two times at which the hour and minute hands will be perpendicular?
Answers
Answer:
The two times are 6:15 and 6:45
Step-by-step explanation:
Given
\(Time = 6\ O'\ clock\)
Required
Next two times which the hour and minute hands are perpendicular
For a time to have perpendicular hands, the difference between the hour and minute hands must be 15 minutes.
Having said that:
15 minutes after 6 O' clock is: 6 : 15 (This is perpendicular)
15 minutes after then is 6 : 30 -- This is not perpendicular
15 minutes after then is 6 : 45 -- This is perpendicular
Hence, the two times are: 6:15 and 6:45
Find the moment of inertia about the y-axis of the thin semicirular region of constant density
Answers
The moment of inertia about the y-axis of the thin semicircular region of constant density is given below.
\(\rm I_y = \dfrac{1}{8} \times \pi r^4\)
What is rotational inertia?Any item that can be turned has rotational inertia as a quality. It's a scalar value that indicates how complex it is to adjust an object's rotational velocity around a certain axis.
Then the moment of inertia about the y-axis of the thin semicircular region of constant density will be
\(\rm I_x = \int y^2 dA\\\\I_y = \int x^2 dA\)
x = r cos θ
y = r sin θ
dA = r dr dθ
Then the moment of inertia about the x-axis will be
\(\rm I_x = \int _0^r \int _0^{\pi} (r\sin \theta )^2 \ r \ dr \ d\theta\\\\\rm I_x = \int _0^r \int _0^{\pi} r^3 \sin ^2\theta \ dr \ d\theta\)
On integration, we have
\(\rm I_x = \dfrac{1}{8} \times \pi r^4\)
Then the moment of inertia about the y-axis will be
\(\rm I_y = \int _0^r \int _0^{\pi} (r\cos\theta )^2 \ r \ dr \ d\theta\\\\\rm I_y = \int _0^r \int _0^{\pi} r^3 \cos ^2\theta \ dr \ d\theta\)
On integration, we have
\(\rm I_y = \dfrac{1}{8} \times \pi r^4\)
Then the moment of inertia about O will be
\(\rm I_o = I_x + I_y\\\\I_o = \dfrac{1}{8} \times \pi r^4 + \dfrac{1}{8} \times \pi r^4\\\\I_o = \dfrac{1}{4} \times \pi r^4\)
More about the rotational inertia link is given below.
https://brainly.com/question/22513079
#SPJ4
i’ve tried to do it but i’m confused and need someone to show me.

Answers
From the given question,
\(x^4+9x^2\)Now,
Put x=-3 into the given expression
\(x^4+9x^2=(-3)^4+9(-3)^2\)\(\begin{gathered} x^4+9x^2=(-3)^4+9(-3)^2 \\ =81+9(9) \\ =81+81 \\ =162 \end{gathered}\)Hence, the option D is correct.
a can do a piece of work in 5 days and b in 8 days. How long will they take to complete the work together
Answers
This is a ratio and proportion problem.
A’s portion of work completed in 6 days.
B’s portion of work completed in 8 days.
Together A+B=1/6+1/8 =7/24 Find Lowest Common Denominator
That means they finish 7/24 ratio of work a day, so now we have to find how long it will take them.
Take 1 day, and divide it by 7/24 ratio of work
1/7/24=24/7=3.43 days to finish.
The larger triangle is a dilation of the smaller triangle with a center of dilation at (1,−1).
What is the scale factor of the dilation?
18
14
4
8

Answers
Answer:
just 4 I think
Step-by-step explanation:
the bottom of the bigger triangle is 8 and the little one is 2
8÷2= 4
Answer: just took the test. the answer is 4!
Step-by-step explanation:
A heavy chair is 3 1/2 feet wide, and Alexis doesn’t want to move it to her new place unless it can pass through the door frame with at least 3 inches to spare. What’s the smallest width that her new door frame can be in order for Alexis to want to move the chair?
Answers
Answer:
3 feet 9 inches or 3 3/4 feetStep-by-step explanation:
The smallest width of the door:
3 1/2 feet + 3 inches = 3 feet 6 inches + 3 inches = 3 feet 9 inchesor
3 9/12 feet = 3 3/4 feetThe smallest width that her new door frame can be is 3 feet 3/4 inches or 3 feet 9 inches.
This will allow Alexis to move the chair through the door with the desired clearance.
Here, we have to ensure that the chair can pass through the door frame with at least 3 inches to spare, we need to find the minimum width of the door frame.
Given that the chair is 3 1/2 feet wide, or 3.5 feet, and Alexis wants at least 3 inches of clearance, we can add the chair's width and the clearance together:
3.5 feet (chair width) + 3 inches (clearance) = 3.5 feet + 0.25 feet = 3.75 feet
So, the door frame should be at least 3.75 feet wide to allow the chair to pass through with at least 3 inches to spare.
However, we can convert 3.75 feet to a mixed number for clarity:
3.75 feet = 3 feet + 0.75 feet = 3 feet + 3/4 feet
Therefore, the smallest width that her new door frame can be is 3 feet 3/4 inches or 3 feet 9 inches.
This will allow Alexis to move the chair through the door with the desired clearance.
To earn more on addition click:
brainly.com/question/29560851
#SPJ3
due 7:59 am est. Faith is saving up to buy a new bicycle. She already has $40 and can save an additional $6 per week using money from her after school job. How much total money would Faith have after 8 weeks of saving? Also, write an expression that represents the amount of money Faith would have saved in w weeks.
Answers
Answer:
After 8 weeks, Faith would have $88. money saved = 40+6w
Answer:
$88 saved in 8 weeks
Step-by-step explanation:
Part 1:
You would first set up the equation 40 + (6 x 8) = t. T would be the total money saved. You would then do 6 times 8 first, as they're in parenthesis. You would get 48. You now have 40 + 48 = t. You would now add like terms, and you would get 88 = t. You would save $88 in 8 weeks.
Part 2:
40 + 6w = t
w would represent the number of weeks, t would represent the total number of money saved.
((16526+828929)÷82727)×0
need step by step explanation
Answers
The value of the equation A = ( ( 16526 + 828929 ) ÷ 82727 ) × 0 is A = 0
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
A = ( ( 16526 + 828929 ) ÷ 82727 ) × 0 be equation (1)
On simplifying the equation , we get
A = ( 8,45,455 ÷ 82727 ) × 0
On further simplification , we get
A = 10.219819405 x 0
Any number multiplied by the number 0 will result in 0
Therefore , the value of A = 0
Hence , the equation is A = 0
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
If a standard die is rolled twice, what is the probability that it lands on a number greater than 4 both times?
Answers
Answer:
1/3 i believe
Step-by-step explanation:
suppose four identical dice are rolled. define an outcome to be a particular combination of four numbers that come up on the four dice. for example, 2, 1, 5, 2 is the same outcome as 1, 2, 2, 5, but not the same as 2, 1, 6, 1 (even though the total is the same). how many different outcomes are possible?
Answers
There are 15 different outcomes possible when rolling four identical dice.
Since each die has six possible outcomes (numbers 1 to 6), the number of different outcomes for a single die is 6.
The total number of different outcomes when rolling four dice, we need to calculate the number of combinations of four elements taken from a set of six elements (one for each die).
This can be calculated using the formula for combinations, given by:
C(n, r) = n! / (r!(n - r)!)
Where, n is the total number of elements (6 in this case) r is the number of elements to be chosen (4 in this case) ! represents the factorial operation
Using this formula, we can calculate the number of different outcomes
C(6, 4) = 6! / (4!(6 - 4)!)
C(6, 4) = 6! / (4!2!)
C(6, 4) = 30 / 2
C(6, 4) = 15
Therefore, there are 15 different outcomes possible when rolling four identical dice.
To know more about outcomes click here :
https://brainly.com/question/2495224
#SPJ4
Evaluate the expression 1/4 x (3/9 + 5)
Choices:1 1/3,1 2/3,5,answer not here.
Answers
Answer:
First option
Step-by-step explanation:
Given the following equation:
\(\frac{1}{4} \times(\frac{3}{9} +5)\)
In order to find the answer, we solve the equation in between the parenthesis according to order of operations and then multiply that answer by 1/4.
\(\frac{1}{4} \times(\frac{3}{9} +5)\)
\(5=\frac{5}{1}\)
\(\frac{3}{9} +\frac{5}{1}\)
\(3\times1=3\)
\(9\times1=9\)
\(5\times9=45\)
\(1\times9=9\)
\(\frac{3}{9} +\frac{45}{9}\)
\(3+45=48=\frac{48}{9}\)
\(\frac{48}{9} \div3=\frac{16}{3}\)
\(\frac{1}{4} \times\frac{16}{3}\)
\(1\times16=16\)
\(4\times3=12\)
\(\frac{16}{12} \div2=\frac{8}{6} \div2=\frac{4}{3}\)
\(\frac{4}{3} =4\div3=1\frac{1}{3}\)
\(=1\frac{1}{3}\)
Hope this helps.
you roll 3 dice. if you get the same number, you earn 10 $. if you get two numbers the same, you get 5 $. if the numbers are all different, you lose 2 $. what is the expected win?
Answers
When you roll 3 dice, if if you get the same number, you earn 10 $. if you get two numbers the same, you get 5 $. if the numbers are all different, you lose $2, the expected win is $1.25.
Given,
You roll 3 dice.
In each dice there will be 6 outcomes
Total number of outcomes = \(6^{3}=216\)
Conditions are
You earn $10, if you get same numbersYou earn $5, if you get two numbers sameYou loss $2, if the numbers are all differentWe can find the number of each cases by using the combination method
Number of cases all the outcomes are same =6
Number of cases you get two numbers same = \(6C_{2}\)×3!
=90
Number of cases the numbers are all different= 6×5×4
=120
Therefore the expected win = (6×10+90×5-120×2)÷216
=270÷216
= $1.25
Hence, when you roll 3 dice, if if you get the same number, you earn 10 $. if you get two numbers the same, you get 5 $. if the numbers are all different, you lose $2, the expected win is $1.25.
Learn more about combination here
brainly.com/question/13387529
#SPJ4
Kai wants to buy a new surfboard. He earns $12.50 each time he mows a lawn. He keeps track of the total amount of money that he has, y, with the equation y-12.5x+30
. The x represents the number of lawns that Kai mows. What does the y-intercept represent in this equation?
A
The cost of the surfboard
B
The number of lawns that Kai mows
C
The total money that Kai will make
D
The money that Kai started with before he mowed any lawns
Answers
Answer:
D. The money that Kai started with before he mowed any lawns.
Step-by-step explanation:
We Know
The equation is y = mx + b
The x represents the number of lawns that Kai mows.
What does the y-intercept represent in this equation?
The y-intercept is when the x = 0, meaning the y-intercept is the amount of money he has when mowing 0 lawn. So, the answer is D.
Answer:
The Answer is D
Step-by-step explanation:
What is the area of the patio if the yard is 12 feet on each side?
How do I do this?
Answers
144 feet squared
Step-by-step explanation:Squares are 4 sided shapes that have an equal length on each side.
Area Formula
The area of a square (or rectangle) is \(l*w\), where \(l\) is the length and \(w\) is the width. Due to the fact that squares have four equal sides, the formula can be rewritten as \(l^2\).
Solving For Area
Plug the length value into the formula.
\(12^2=144\)Then, add the units to the answer. Because the length is multiplied by itself and the original unit is feet, the units are feet squared.
A soft drink vendor at a popular beach analyzes his sales records and finds that if he sells xcans of soda pop in one day, his profit (in dollars) is given by P(x) 0.001x2 3x 1800 What is his maximum profit per day, and how many cans must he sell to reach the maximum profit?
Answers
The soft drink vendor's maximum profit per day is $5250, and he must sell 1500 cans of soda pop to reach the maximum profit.
To find the maximum profit per day for the soft drink vendor, we need to use the formula P(x) = 0.001x^2 + 3x + 1800, where x is the number of cans of soda pop sold in one day.
To find the maximum profit, we need to find the vertex of the parabola represented by the profit function. The x-coordinate of the vertex is given by -b/2a, where a = 0.001 and b = 3. Plugging in these values, we get x = -3/(2*0.001) = -1500.
Since the soft drink vendor cannot sell a negative number of cans, we know that the maximum profit occurs at the closest whole number to x = -1500, which is x = 1500.
To find the maximum profit per day, we can plug in x = 1500 into the profit function:
P(1500) = 0.001(1500)^2 + 3(1500) + 1800 = $5250
Therefore, the soft drink vendor's maximum profit per day is $5250, and he must sell 1500 cans of soda pop to reach the maximum profit.
To find the maximum profit per day and the number of cans needed to reach that profit, we'll first need to find the critical point of the given quadratic profit function, P(x) = -0.001x^2 + 3x - 1800.
Step 1: Find the derivative of P(x) with respect to x. This will give us the rate of change of profit as the number of cans sold changes.
P'(x) = -0.002x + 3
Step 2: Set the derivative equal to zero and solve for x. This will give us the critical point where the maximum profit occurs.
-0.002x + 3 = 0
x = 1500 cans
Step 3: Substitute the critical point (x = 1500) back into the profit function P(x) to find the maximum profit.
P(1500) = -0.001(1500)^2 + 3(1500) - 1800
P(1500) = $600
So, the maximum profit per day is $600, and the soft drink vendor must sell 1500 cans to reach the maximum profit.
Learn more about profit at: brainly.com/question/15699405
#SPJ11
The maximum profit per day is $4800, and the vendor must sell 1500 cans of soda pop to reach this maximum profit.
The profit function for the soft drink vendor is given by:
P(x) = \(0.001x^2 + 3x + 1800\)
To find the maximum profit, we need to find the vertex of the parabola represented by this function. The x-coordinate of the vertex can be found using the formula:
x = -b / (2a)
where a = 0.001 and b = 3. Substituting these values, we get:
x = -3 / (2 * 0.001) = -1500
Since the value of x cannot be negative in this context, we know that the maximum profit occurs at x = 1500. To find the maximum profit, we substitute this value of x into the profit function:
P(1500) =\(0.001(1500)^2 + 3(1500) + 1800 = $4800\)
Therefore, the maximum profit per day is $4800, and the vendor must sell 1500 cans of soda pop to reach this maximum profit.
Learn more about maximum profit
https://brainly.com/question/29248429
#SPJ4
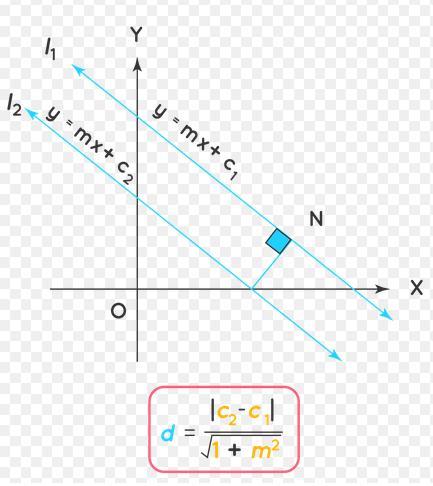
Find the distance between the parallel lines y=2x+1 and 2y=4x-3
Answers
Answer:
Step-by-step explanation:
\(y=2x+1\)
\(2y=4x-3\rightarrow y=2x-\frac{3}{2}\)
\(d=\frac{|1-(-\frac{3}{2} )|}{\sqrt{1+2^2} }\)
\(=\frac{(\frac{5}{2} )}{\sqrt{5} }\)
\(=\frac{5}{2\sqrt{5} }\)
\(=\frac{5}{2\sqrt{5} }\times \frac{\sqrt{5}}{\sqrt{5} }\) (this is to rationalize the denominator...tidies it up.)
\(=\frac{5\sqrt{5} }{2\times5 }\)
\(=\frac{\sqrt{5} }{2 }\)
5. 3x = 6. 40x how many time do I need to multiply thee number for them to be the ame
Answers
The equation 3x = 6.4 can be solved for x by dividing both sides of the equation by 3: 3x/3 = 6.4/3; x = 2.13
So, for 3x and 6.4x to be equal, x must be equal to 2.13. This means that you need to multiply the number 6.4 by 2.13 to equal 3. The equation 3x = 6.4 represents the relationship between two variables, x and 3x. We are trying to find the value of x that would make 3x equal to 6.4. To do this, we divide both sides of the equation by 3. Dividing both sides of an equation by the same number does not change the relationship between the variables; it only scales down the variable's value by the same factor.
So, by dividing both sides of the equation by 3, we get:
3x/3 = 6.4/3
x = 2.13
Finally, to make 6.4x equal to 3, we need to divide 6.4 by 2.13: 6.4 / 2.13 = 3. So, we need to multiply 6.4 by 2.13 to equal 3.
To learn more about equation, visit here
https://brainly.com/question/29657983
#SPJ4
a buyer purchased 8 blue shirts and X red shirts. The ratio of blue shirts to red shirts purchased was 2:5. How many red shirts did the buyer purchase?
Answers
Answer:
20
Step-by-step explanation:
b:r
2:5
8:x 8/2=4
5*4=20
The price at an item has been reduced by $3.49. The original price was $66.75. What is the price now?
Answers
Answer:
i need help
Step-by-step explanation:
waaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
which property is used in the following expression (a.b) .c=a.(b.c) commutative of property of addition distributive property associative property of multiplication associative property of addition
Answers
Commutative Property:
The commutative property is a math rule that says that the order in which we multiply numbers does not change the product
a.b = b.a
Distributive Property:
The distributive property is express as:
\(a\cdot(b+c)=a\cdot b+a\cdot c\)Associative Property of Multiplication:
It express as :
\(a\cdot(b\cdot c)=(a\cdot b)\cdot c\)Associative Property of Addition:
It express as:
\(a+(b+c)=(a+b)+c\)So, the given property is the associative multiplication
Answer : c) associative property of multiplication
.
Look over Chuck's work What is incorrect about the way Chuck interpreted his problem? What should have been a clue to Chuck that something was wrong?

Answers
The probability that a random student will be taking both Algebra 2 and Chemistry is 0.0136 or 1.36%.
To find the probability that a random student will be taking both Algebra 2 and Chemistry, we need to use the concept of conditional probability.
Let's denote the event of taking Algebra 2 as A and the event of taking Chemistry as C. We are given that P(A) = 0.08 (8% probability of taking Algebra 2) and P(C|A) = 0.17 (17% probability of taking Chemistry given that the student is taking Algebra 2).
The probability of taking both Algebra 2 and Chemistry can be calculated using the formula for conditional probability:
P(A and C) = P(C|A) * P(A)
Substituting the given values:
P(A and C) = 0.17 * 0.08
P(A and C) = 0.0136
Therefore, the probability that a random student will be taking both Algebra 2 and Chemistry is 0.0136 or 1.36%.
It is important to note that the probability of taking both Algebra 2 and Chemistry is determined by the intersection of the two events, which means students who are taking both courses. In this case, the probability is relatively low, as it depends on the individual probabilities of each course and the conditional probability given that a student is taking Algebra 2.
For more such questions on probability visit:
https://brainly.com/question/25839839
#SPJ8
What is the domain of this quadratic function?

Answers
The graph goes on forever in both directions along the x axis. This indicates any x value can be plugged into the quadratic to get some y output. There are no restrictions. The domain is the set of all possible x inputs of a function.
i need help fast please

Answers
Answer:
The answer is 540 mm^3
Step-by-step explanation:
using v= BH
v= 30×18
v= 540mm^3
pls like and follow, hope this helps.:-):-)
Using the following graph, determine the slope of the line,

Answers
Answer:
-2
Step-by-step explanation:

Answer:
Start at 10 and do rise over run. Rise over how many numbers (spaces) and run over how many plots.
Solve 9^4x+4=243^2x+2.
Answers
6561x + 4 = 59049x +2
6561x = 59049x +2 -4
6561x = 59049x -2
-2 = 6561x - 59049x
-2 = - 52488x
X= 2/52488
X = 1/ 26244
can you show me how to solve this it is angles in a triangle

Answers
Vertical angles are two non-adjacent angles formed by intersecting two lines. The intersection forms two pair of vertical angles. And it is true that:
\(\begin{gathered} x=40 \\ y=z \end{gathered}\)For the green triangle, we can use the triangle sum theorem, which states that the sum of the internal angles of a triangle is equal to 180, so:
\(\begin{gathered} x+y+35=180 \\ 40+y+35=180 \\ \text{solve for y:} \\ y+75=180 \\ y=180-75 \\ y=105 \end{gathered}\)Using the same theorem for the blue triangle:
\(\begin{gathered} w+105+49=180 \\ w+154=180 \\ w+154=180 \\ \text{solve for w:} \\ w=180-154 \\ w=26 \end{gathered}\)? = w, therefore, ? = 26
