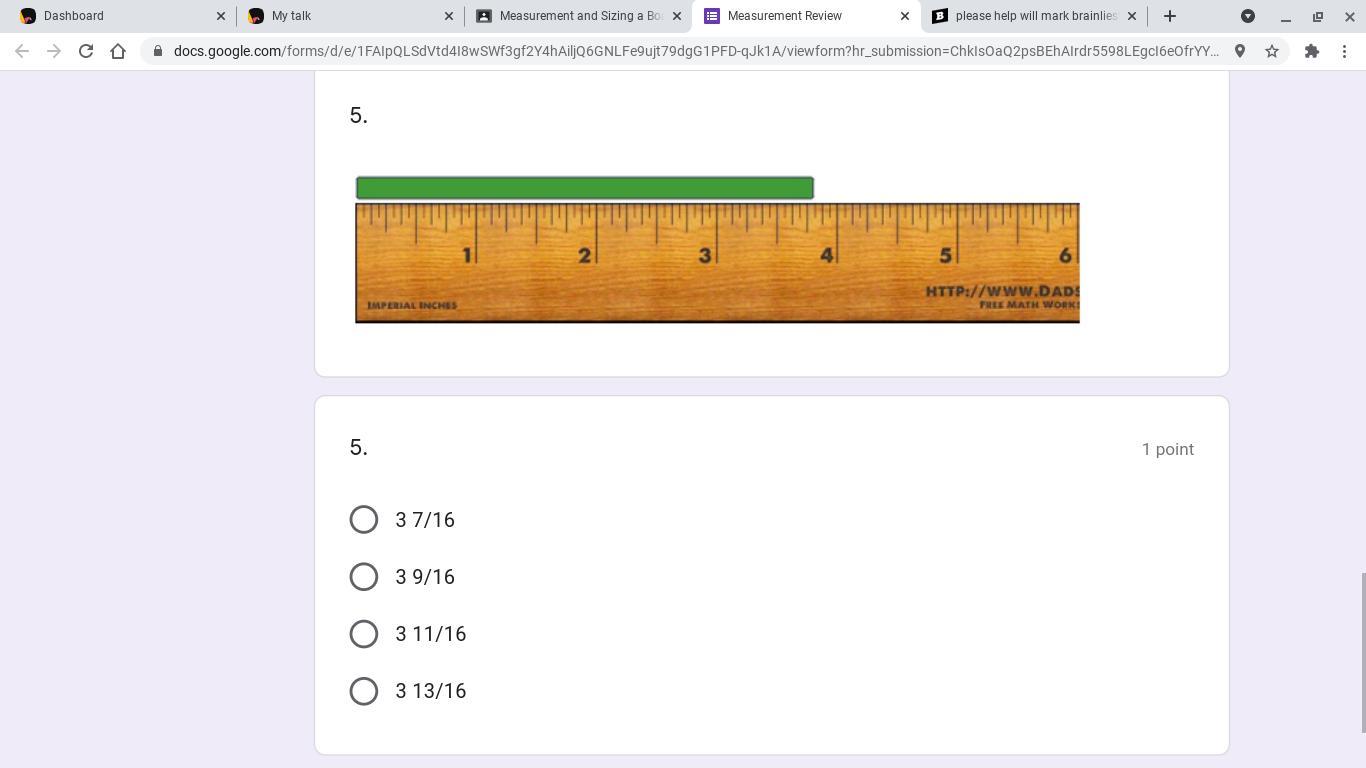
Answers
Answer:
D
Step-by-step explanation:
count the marks on the ruler to 13/16
Related Questions
Can someone please help me with writing a flowchart proof?

Answers
The two triangles are equivalent triangles
Flowchart proofs are organized with boxes and arrows.
The statements given are written in the box and the reason of that statement is written just below the box.
Every statement if flowchart proof complements other statement.
The correct answer is
∠AZ = ∠BX
The two triangles are equivalent triangles.
Learn more at https://brainly.com/question/24319270
The average yearly rainfall in Lakeview is 21.62 inches. What is the total amount of rainfall in inches, in Lakeview in 5.5 years answer choices 118.91 inches 216.10 inches 27.12 inches 16.12 inches
Answers
Answer: 118.91 inches
Step-by-step explanation:
From the question, we are informed that the average yearly rainfall in Lakeview is 21.62 inches.
To calculate the total amount of rainfall in inches, in Lakeview in 5.5 years, we multiply 21.62 by 5.5. This will be:
= 21.62inches × 5.5
= 118.91 inches
3 of 10
What is the decimal multiplier to decrease by 25%?
Answers
Answer:
0.75
Step-by-step explanation:
decrease by 25% means multiply by 75%
convert 75%to decimal
75/100=0.75
5. The set of ordered pairs shown below defines a
relation.
{(0, 2), (1,4), (2,6), (3, 8), (4, 10)}
What is the value of the greatest element in the
range of this relation?
Answers
Answer:
10
Step-by-step explanation:
here the range are (2,4,6,8,10)
and the value of the greatest element in the range is 10.
What is the quotient when the whole number 8 is divided by the fraction 1/6
Answers
Answer:
48
Step-by-step explanation:
You put 8/1 divided by 1/6 and multiply by the reciprocal. Then you get 8/1*6/1 which equals 48/1. 48/1 is equal to 48.
Given:
Prove:
Three lines AD, CF, and BE are intersecting each other at the midpoint O
Complete the proof.
It is given that
and
. By the
,
. Therefore,
. By the
,
, and by the
,
. After application of the
,
.
Answers
∠CFA ≅ ∠EDA (By Transitive Property of Congruence).
Given:
Three lines AD, CF, and BE are intersecting each other at the midpoint O.
To prove:
∠CFA ≅ ∠EDA
Proof:
Given that AD, CF, and BE intersect at the midpoint O.
By definition of a midpoint, OA ≅ OD, OB ≅ OE.
OA = OD and OB = OE.
Triangle OAD ≅ Triangle OBE (By Side-Side-Side congruence).
∠OAD ≅ ∠OBE (By Corresponding Parts of Congruent Triangles are Congruent).
∠CFA and ∠EDA are vertical angles.
∠OAD ≅ ∠CFA and ∠OBE ≅ ∠EDA (By Vertical Angles are Congruent).
Therefore, ∠CFA ≅ ∠EDA (By Transitive Property of Congruence).
Hence, it is proven that ∠CFA ≅ ∠EDA.
for such more question on Congruence
https://brainly.com/question/1675117
#SPJ8
Determine the length of AC

Answers
Answer:
(a) 16.7 units
Step-by-step explanation:
You want the length of the side opposite the angle 68° in a triangle with a side of length 18 opposite the angle 86°.
Law of sinesThe law of sines tells you side lengths are proportional to the sine of the opposite angle:
AC/sin(B) = BC/sin(A)
AC = BC·sin(B)/sin(A)
Angle B is a little more than 3/4 of angle A, so the ratio of sines will be more than that value, but less than 1. This tells you AC < (3/4)BC, eliminating choices b, c, d.
The length of AC is about 16.7 units.
__
Additional comment
If you put the numbers into the expression for AC and do the math, you find AC ≈ 16.7301° ≈ 16.7, as we estimated.
68/86 ≈ 0.7907
sin(68)/sin(86) ≈ 0.9294
The ratio of sines of angles versus the angle ratio is only a good match for small angles (generally 5° or less). Otherwise, the ratio of the smallest to largest angle will always be less than the ratio of their sines. (This is because the sine function has decreasing slope for first-quadrant angles.)
<95141404393>
the chi-square distribution provides a good approximation to the sampling distribution of the chi-square statistic if the expected frequency in each cell is
Answers
The chi-square distribution provides a good approximation to the sampling distribution of the chi-square statistic if the expected frequency in each cell is at least 5.
The chi-square statistic is a measure of how different an observed frequency is from the expected frequency. It is calculated by taking the difference between the observed and expected frequency in each cell, squaring it, and then summing the results. This measure can then be compared to a chi-square distribution with degrees of freedom equal to the number of cells minus one. If the calculated statistic is larger than the expected value from the chi-square distribution, then it can be concluded that the observed frequency differs significantly from the expected frequency.
In order to use the chi-square approximation, it is important that the expected frequency in each cell is at least 5. This is because the chi-square approximation only works well when there are large expected frequencies. When expected frequencies are smaller than 5, the chi-square statistic is not an accurate measure of the difference between the observed and expected frequencies.
For more such questions on chi-square distribution
https://brainly.com/question/4543358
#SPJ11
Simplify 4x/5+x/6x/x+2

Answers
\(\\ \tt\longmapsto \dfrac{4x}{5+x}\div \dfrac{6x}{x+2}\)
\(\\ \tt\longmapsto \dfrac{4x}{5+x}\times \dfrac{x+2}{x}\)
\(\\ \tt\longmapsto 4x^2=x^2+7x+10\)
\(\\ \tt\longmapsto 4x^2-x^2-7x-10=0\)
\(\\ \tt\longmapsto 3x^2-7x-10=0\)
The value of the Expression is = 2(x+2)/3(x+5)
What is an Expression?Mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Given an Expression, 4x/(x+5)/6x/(x+2)
4x/(x+5)/6x/(x+2)
= 4x/(x+5)*(x+2)/6x
= 2(x+2)/3(x+5)
Hence, the value of the Expression is 2(x+2)/3(x+5)
For more references on Expression, click;
https://brainly.com/question/14083225
#SPJ2
Consider the function where xy U = for (x, y) = (0,0), x² + y² and v= = 0 for all x and y. X 2.1 Show that all partial derivatives of u and v exist at (x, y) = (0, 0), and thus satisfy the Cauchy- Riemann equations. (5) 2.2 Show that is not continuous at (0,0), and hence f is not differentiable at (0, 0). U (5) 2.3 Investigate whether f is analytic or not. (5) 2.4 Investigate whether f has a harmonic complex conjugate or not. (5) 2.5 Show that the function f (x, y) = x² - y² —y is harmonic and determine its harmonic conjugate. - f = u + iv,
Answers
2.1 To show that all partial derivatives of u and v exist at (x, y) = (0, 0) and satisfy the Cauchy-Riemann equations, we need to calculate the partial derivatives of u and v and check their existence and the Cauchy-Riemann conditions.
The function is given as u(x, y) = xy and v(x, y) = x² + y².
Partial derivatives of u:
∂u/∂x = y
∂u/∂y = x
Partial derivatives of v:
∂v/∂x = 2x
∂v/∂y = 2y
All partial derivatives exist at (x, y) = (0, 0) since they are simple functions and do not have any singularities.
Now, let's check if the Cauchy-Riemann equations are satisfied:
∂u/∂x = ∂v/∂y
y = 2y
This equation holds true for all values of y, including y = 0.
∂u/∂y = -∂v/∂x
x = -2x
This equation also holds true for all values of x, including x = 0.
Therefore, all partial derivatives of u and v exist at (x, y) = (0, 0), and they satisfy the Cauchy-Riemann equations.
2.2 To show that f is not continuous at (0, 0) and hence not differentiable at (0, 0), we can examine the behavior of f as (x, y) approaches (0, 0).
The function f(x, y) = u(x, y) + iv(x, y) = xy + i(x² + y²)
As (x, y) approaches (0, 0), both u(x, y) = xy and v(x, y) = x² + y² approach 0. However, f(x, y) = xy + i(x² + y²) approaches 0 + i(0) = i(0) = 0i = 0, which is a different value.
Therefore, f is not continuous at (0, 0), and hence it is not differentiable at (0, 0).
2.3 To investigate whether f is analytic or not, we need to check if it is differentiable in a neighborhood around every point.
Since we have already shown that f is not differentiable at (0, 0), it implies that f is not analytic because differentiability is a necessary condition for analyticity.
2.4 To investigate whether f has a harmonic complex conjugate or not, we need to check if u and v satisfy the Laplace's equation (∇²u = 0 and ∇²v = 0) and if they satisfy the Cauchy-Riemann equations.
The Laplace's equation is not satisfied by u(x, y) = xy because ∇²u = ∂²u/∂x² + ∂²u/∂y² = 0 + 0 ≠ 0.
Therefore, f does not have a harmonic complex conjugate.
2.5 To show that the function f(x, y) = x² - y² - iy is harmonic, we need to demonstrate that it satisfies the Laplace's equation (∇²u = 0 and ∇²v = 0).
For u(x, y) = x² - y², we have ∇²u = ∂²u/∂x² + ∂²u/∂y² = 2 - 2 = 0.
For v(x, y) = -y, we have ∇²v = ∂²v/∂x² + ∂²v/∂y² = 0 + 0 = 0.
Both u and v satisfy the Laplace's equation, indicating that f(x, y) = x² - y² - iy is a harmonic function.
To determine the harmonic conjugate of f, we can integrate the partial derivative of v with respect to x and y, and obtain the imaginary part of the function:
h(x, y) = ∫ (∂v/∂y) dy = ∫ 0 dy = C(y)
Where C(y) is an arbitrary function of y.
The harmonic conjugate of f is given by:
g(x, y) = u(x, y) + ih(x, y) = x² - y² + iC(y)
Therefore, the harmonic conjugate of f(x, y) = x² - y² - iy is g(x, y) = x² - y² + iC(y), where C(y) is an arbitrary function of y.
Learn more about Cauchy-Riemann here -: brainly.com/question/30385079
#SPJ11
To show that all partial derivatives of u and v exist at (x, y) = (0, 0) and satisfy the Cauchy-Riemann equations, we need to calculate the partial derivatives of u and v and check their existence and the Cauchy-Riemann conditions.
The function is given as u(x, y) = xy and v(x, y) = x² + y².
Partial derivatives of u:
∂u/∂x = y
∂u/∂y = x
Partial derivatives of v:
∂v/∂x = 2x
∂v/∂y = 2y
All partial derivatives exist at (x, y) = (0, 0) since they are simple functions and do not have any singularities.
Now, let's check if the Cauchy-Riemann equations are satisfied:
∂u/∂x = ∂v/∂y
y = 2y
This equation holds true for all values of y, including y = 0.
∂u/∂y = -∂v/∂x
x = -2x
This equation also holds true for all values of x, including x = 0.
Therefore, all partial derivatives of u and v exist at (x, y) = (0, 0), and they satisfy the Cauchy-Riemann equations.
2.2 To show that f is not continuous at (0, 0) and hence not differentiable at (0, 0), we can examine the behavior of f as (x, y) approaches (0, 0).
The function f(x, y) = u(x, y) + iv(x, y) = xy + i(x² + y²)
As (x, y) approaches (0, 0), both u(x, y) = xy and v(x, y) = x² + y² approach 0. However, f(x, y) = xy + i(x² + y²) approaches 0 + i(0) = i(0) = 0i = 0, which is a different value.
Therefore, f is not continuous at (0, 0), and hence it is not differentiable at (0, 0).
2.3 To investigate whether f is analytic or not, we need to check if it is differentiable in a neighborhood around every point.
Since we have already shown that f is not differentiable at (0, 0), it implies that f is not analytic because differentiability is a necessary condition for analyticity.
2.4 To investigate whether f has a harmonic complex conjugate or not, we need to check if u and v satisfy the Laplace's equation (∇²u = 0 and ∇²v = 0) and if they satisfy the Cauchy-Riemann equations.
The Laplace's equation is not satisfied by u(x, y) = xy because ∇²u = ∂²u/∂x² + ∂²u/∂y² = 0 + 0 ≠ 0.
Therefore, f does not have a harmonic complex conjugate.
2.5 To show that the function f(x, y) = x² - y² - iy is harmonic, we need to demonstrate that it satisfies the Laplace's equation (∇²u = 0 and ∇²v = 0).
For u(x, y) = x² - y², we have ∇²u = ∂²u/∂x² + ∂²u/∂y² = 2 - 2 = 0.
For v(x, y) = -y, we have ∇²v = ∂²v/∂x² + ∂²v/∂y² = 0 + 0 = 0.
Both u and v satisfy the Laplace's equation, indicating that f(x, y) = x² - y² - iy is a harmonic function.
To determine the harmonic conjugate of f, we can integrate the partial derivative of v with respect to x and y, and obtain the imaginary part of the function:
h(x, y) = ∫ (∂v/∂y) dy = ∫ 0 dy = C(y)
Where C(y) is an arbitrary function of y.
The harmonic conjugate of f is given by:
g(x, y) = u(x, y) + ih(x, y) = x² - y² + iC(y)
Therefore, the harmonic conjugate of f(x, y) = x² - y² - iy is g(x, y) = x² - y² + iC(y), where C(y) is an arbitrary function of y.
Learn more about Cauchy-Riemann here -: brainly.com/question/30385079
#SPJ11
Question 1-27
Which set of values is the solution set of the equation [2x-31 = 7?
(2, 5)
O (2.-5)
O 1-2, 5)
0 (-2,-5)

Answers
The equation be |2x-3| = 7 then the set of values is the solution set be (2, -5).
What is meant by equation?An equation is a mathematical statement that proves two mathematical expressions are equal in algebra, and this is how it is most commonly used. When two expressions are joined by an equal sign, a mathematical statement is called an equation.
In mathematics, to solve an equation is to identify its solutions, which are the values (numbers, functions, sets, etc.) that satisfy the requirement expressed by the equation. An equation typically consists of two expressions connected by an equals sign. A variable or variables are labeled as unknowns when looking for a solution.
Any combination of a number, a variable, and operation symbols is considered an expression. Two expressions are combined to form an equation, which is joined by the equal sign.
Let the equation be |2x-3| = 7
We know that if \($|a|=b, a=\pm b$\).
Since we do not know if 2x - 3 exists positive or negative, we will need a \($\pm$\) on the 7 :
\($|2 x-3|=7 \Rightarrow 2 x-3=\pm 7$$\)
Add 3 to both sides, and finally divide by 2, we get
\($$\begin{aligned}& 2 x=3 \pm 7 \\& x=\frac{3}{2} \pm \frac{7}{2}\end{aligned}$$\)
So x exists equal to either 10/2 = 5 or -4/2 = -2.
Therefore, the correct answer is option b) (2, -5).
To learn more about equations refer to:
https://brainly.com/question/2228446
#SPJ1
I need help with this Graph!
Graph a right triangle with the two points forming the hypotenuse. Using the sides, find the distance between the two points, to the nearest tenth (if necessary). (-6,3) and (3, -9)
find leg number 1 and leg number 2 and the distance

Answers
Answer:
Step-by-step explanation:

The distance between two points (-6, 3) and (3, -9) is 10.81 units.
We have a graph a right triangle with the two points A(-6,3) and B(3, -9) forming the hypotenuse.
We have find the distance between the two points using only the sides of the right triangle.
What is the formula to find the distance between the two points on Cartesian plane ?The distance between two points -
\(d = \sqrt {\left( {x_1 - x_2 } \right)^2 + \left( {y_1 - y_2 } \right)^2 }\)
According to the question, we have -
Coordinates of Point A = (- 6, 3)
Coordinates of Point C = (3, -9)
Now -
Coordinates of Point B will be (- 6, -9) [formed by the intersection of sides].
Distance AB -\(AB = \sqrt {\left( {-6 - (-6) } \right)^2 + \left( {3 - (-9 } \right)^2 }\) = 6 units
Distance BC -\(BC = \sqrt {\left( {-6 - 3 } \right)^2 + \left( {-9 - (-9 } \right)^2 }\) = 9 units
Using the Pythagoras theorem -
\((AC)^{2} =(AB)^{2} +(BC)^{2}\)
\((AC)^{2} =\) 36 + 81
AC = \(\sqrt{117}\) = 10.81
Hence, the distance between two points (-6, 3) and (3, -9) is 10.81 units.
To solve more questions on Distance formula, visit the link below -
brainly.com/question/12662141
#SPJ6

What is the value of −3 + |−17|?
20
14
−14
−20
Answers
Answer:
b) 14
Step-by-step explanation:
Given problem,
→ -3 + |-17|
Let's solve the problem,
→ -3 + |-17|
→ -3 + 17
→ 14
Hence, the answer is 14.
Jamie has 105 pieces of candy leftover from Halloween. She would like to distribute them evenly to the 7 kids on her block. Write an equation to show how many pieces of candy each kid will receive.
Answers
Answer:
105/7=15
Step-by-step explanation:
equations have equal signs
a local bbq restaurants offers 2 side dishes with a lunch plate. there are 7 side dishes. how many choices of side dishes does a customer have? note: there is no requirement that the customer chooses different side dishes (i.e. he or she can choose say baked beans twice as their side dish).
Answers
The number of choice out of 7 that consumer have are 42.
What is permutation?The term permutation alludes to a numerical computation of the quantity of ways a specific set can be sorted out. Set forth plainly, a change is a word that depicts the quantity of ways things can be requested or organized. With stages, the request for the course of action matters.
According to given data:Number of choices of side dishes does a customer have,
total dishes(n)=7 , r = 2
ⁿP₂
⁷P₂
7×6 = 42
Thus required number of ways are 42.
To know more about permutation visit:
brainly.com/question/13715183
#SPJ4
Write the value of
\(1 - 2 \cos {}^{2} c\)
Answers
Step-by-step explanation:
1-2cos²c.
> (cos²c+sin²c)-2cos²c. (cos²c+sin²c=1)
> cos²c+sin²c-2cos²c
> sin²c-cos²c.
is your correct answer.
hope this helps you.
the degenerative disease osteoarthritis most frequently affects weight-bearing joints such as the knee. an article presented the following summary data on stance duration (ms) for samples of both older and younger adults. age n sample mean sample sd older 28 801 117 younger 16 780 72 assume that both stance duration distributions are normal. a) calculate and interpret a 99% confidence interval (ci) for true average stance duration among elderly individuals. b) carry out a test of hypotheses to decide whether true average stance duration is larger among elderly individuals than among younger individuals. c) construct a 95% ci for the difference in means and compare results to part(b).
Answers
We are 99% confident that the true average stance duration among elderly individuals lies within the range of 744.56 ms to 857.44 ms.
To test whether the true average stance duration is larger among elderly individuals than among younger individuals, we can perform a one-tailed independent samples t-test. The null hypothesis (H0)
Using the t-test, we compare the means and standard deviations of the two samples and calculate the test statistic
a) To calculate a 99% confidence interval for the true average stance duration among elderly individuals, we can use the sample mean, sample standard deviation, and the t-distribution.
Given:
Older adults: n = 28, sample mean = 801, sample standard deviation = 117
Using the formula for a confidence interval for the mean, we have:
Margin of error = t * (sample standard deviation / √n)
Since the sample size is relatively large (n > 30), we can use the z-score instead of the t-score for a 99% confidence interval. The critical z-value for a 99% confidence level is approximately 2.576.
Calculating the margin of error:
Margin of error = 2.576 * (117 / √28) ≈ 56.44
The confidence interval is then calculated as:
Confidence interval = (sample mean - margin of error, sample mean + margin of error)
Confidence interval = (801 - 56.44, 801 + 56.44) ≈ (744.56, 857.44)
b) To test whether the true average stance duration is larger among elderly individuals than among younger individuals, we can perform a one-tailed independent samples t-test.
The null hypothesis (H0): The true average stance duration among elderly individuals is equal to or less than the true average stance duration among younger individuals.
The alternative hypothesis (Ha): The true average stance duration among elderly individuals is larger than the true average stance duration among younger individuals.
. With the given data, perform the t-test and obtain the p-value.
c) To construct a 95% confidence interval for the difference in means between older and younger adults, we can use the formula for the confidence interval of the difference in means.
Given:
Older adults: n1 = 28, sample mean1 = 801, sample standard deviation1 = 117
Younger adults: n2 = 16, sample mean2 = 780, sample standard deviation2 = 72
Calculating the standard error of the difference in means:
Standard error = √((s1^2 / n1) + (s2^2 / n2))
Standard error = √((117^2 / 28) + (72^2 / 16)) ≈ 33.89
Using the t-distribution and a 95% confidence level, the critical t-value (with degrees of freedom = n1 + n2 - 2) is approximately 2.048.
Calculating the margin of error:
Margin of error = t * standard error
Margin of error = 2.048 * 33.89 ≈ 69.29
The confidence interval is then calculated as:
Confidence interval = (mean1 - mean2 - margin of error, mean1 - mean2 + margin of error)
Confidence interval = (801 - 780 - 69.29, 801 - 780 + 69.29) ≈ (-48.29, 38.29)
Comparison with part (b): In part (b), we performed a one-tailed test to determine if the true average stance duration among elderly individuals is larger than among younger individuals. In part (c), the 95% confidence interval for the difference in means (-48.29, 38.29) includes zero. This suggests that we do not have sufficient evidence to conclude that the true average stance duration is significantly larger among elderly individuals compared to younger individuals at the 95% confidence level.
Know more about 99% confident here:
https://brainly.com/question/30762304
#SPJ11
Suppose that the distance of fly balls hit to the outfield (in baseball) is normally distributed with a mean of 264 feet and a standard deviation of 43 feet. Let X be the distance in feet for a fly ball.
Answers
Given that the distance of fly balls hit to the outfield follows a normal distribution with a mean of 264 feet (μ = 264) and a standard deviation of 43 feet (σ = 43).
we can denote X as the random variable representing the distance in feet for a fly ball.
Therefore, we can express this mathematically as:
X ~ N(264, 43^2)
This notation indicates that X is normally distributed with a mean of 264 and a variance of 43^2.
Learn more about distribution here:
https://brainly.com/question/29664127
#SPJ11
9. Construct Arguments Write a two-column
proof for the Angle Bisector Theorem. MP.3
Answers
The angle bisector theorems is proved below.
What is the angle bisector theorems?It should be noted that the angle bisector theorem simply states that an angle bisector of a triangle divides the opposite side into two segments which are proportional to the other sides of the triangle.
The way to proof the theorem is illustrated:
Draw a ray CX parallel to AD and then extend BA to intersect this ray at E.
In triangle CBE, DA is parallel to CE.
BD/DC == BA/AE ......... i
Now we want to prove that AE = AC
Since DA is parallel to CE, we have:
DAB = CEA (corresponding angles) ....... ii
DAC = ACE (alternate interior angles) ...... iii
Since AD is the bisector of BAC, we've DAB = DAC.
From the above, ACE makes and isosceles triangle and since the opposite sides are equal, we've AC = CE.
Substitute AC for AE in equation i
BD/DC = BA/AC
Therefore, the angle bisector theorems is proved.
Learn more about theorems on:
brainly.com/question/343682
#SPJ1

what is 1/3 + 1/5 as a fraction in simplest form?
Answers
Answer:
8/15
Step-by-step explanation:
find the common denominator, which is 15 and times 1/3 by 5/5 to get 5/15 and times 1/5 by 3/3 to get 3/15 and add them together to get 8/15
The simplest form of the given expression is "\(\frac{8}{15}\)". A further solution of the given expression is provided below.
The given expression is:
→ \(\frac{1}{3} +\frac{1}{5}\)
By taking L.C.M we can solve the above expression, such as:
→ \(\frac{5+3}{15}\)
→ \(\frac{8}{15}\)
Thus the above answer is the appropriate one.
Learn more about fraction here:
https://brainly.com/question/8763270

help please! anyone know how to graph this

Answers
Answer:
The grpah should help!

Answer:
See attached for graph of the given function.
Step-by-step explanation:
Vertex form of a quadratic function
\(f(x)=a(x-h)^2+k\)
where:
(h, k) is the vertex.a is some constant to be found.If a>0 the parabola opens upwards.
If a<0 the parabola opens downwards.
Given function:
\(g(x)=-\dfrac{1}{5}(x+5)^2-2\)
Vertex
Comparing the given function with the vertex formula:
\(\implies h=-5\)
\(\implies k=-2\)
Therefore, the vertex of the parabola is (-5, -2).
As a<0, the parabola opens downwards. Therefore, the vertex is the maximum point of the curve.
Axis of symmetry
The axis of symmetry is the x-value of the vertex.
Therefore, the axis of symmetry is x = -5.
y-intercept
To find the y-intercept, substitute x = 0 into the given function:
\(\implies f(0)=-\dfrac{1}{5}(0+5)^2-2=-7\)
Therefore, the y-intercept is (0, -7).
x-intercepts
To find the x-intercepts, set the function to zero and solve for x:
\(\implies -\dfrac{1}{5}(x+5)^2-2=0\)
\(\implies -\dfrac{1}{5}(x+5)^2=2\)
\(\implies (x+5)^2=-10\)
As we cannot square root a negative number, the curve does not intercept the x-axis.
Additional points on the curve
As the axis of symmetry is x = -5 and the y-intercept is (0, -7), this means that substituting values of x in multiples of 5 either side of the axis of symmetry will yield integers:
\(\implies f(-10)=-\dfrac{1}{5}(-10+5)^2-2=-7\)
\(\implies f(5)=-\dfrac{1}{5}(5+5)^2-2=-22\)
\(\implies f(-15)=-\dfrac{1}{5}(-15+5)^2-2=-22\)
Therefore, plot:
vertex = (-5, -2)y-intercept = (0, -7)points on the curve = (-10, -7), (5, -22) and (-15, -22)axis of symmetry: x = -5Draw a smooth curve through the points, using the axis of symmetry to ensure the parabola is symmetrical.

Zahid is paid a set wage of $774.72 for a 36-hour week, plus time-and-a-half for overtime. In one particular week, he worked 43 hours. What were Zahid’s earnings?
Samantha is paid a set wage of $962.50 for a 35-hour week, plus double time for overtime. In one particular week, she worked 40 hours. What were Samantha’searnings?
Answers
Therefore, Zahid earned $1,001.16 in that particular week in hour and Samantha earned $1,237.50 in that particular week.
What do you mean by hour?An hour is a unit of time measurement that represents a duration of 60 minutes or 3,600 seconds. It is commonly used to measure time in various contexts, such as work schedules, meetings, and appointments. The abbreviation for hour is "hr" or "h".
Given by the question.
For Zahid:
Regular wage per hour = $774.72 / 36 hours = $21.52/hour
Overtime wage per hour = 1.5 x $21.52 = $32.28/hour
Zahid worked 7 hours of overtime (43 - 36 = 7)
Zahid's earnings for the week would be:
Regular earnings = 36 hours x $21.52/hour = $775.20
Overtime earnings = 7 hours x $32.28/hour = $225.96
Total earnings = Regular earnings + Overtime earnings = $1,001.16
For Samantha:
Regular wage per hour = $962.50 / 35 hours = $27.50/hour
Overtime wage per hour = 2 x $27.50 = $55/hour
Samantha worked 5 hours of overtime (40 - 35 = 5)
Samantha's earnings for the week would be:
Regular earnings = 35 hours x $27.50/hour = $962.50
Overtime earnings = 5 hours x $55/hour = $275
Total earnings = Regular earnings + Overtime earnings = $1,237.50
To learn more about hour:
https://brainly.com/question/13533620
#SPJ1
In a carnival game, a player spins a wheel that stops with the pointer on one {and only cne) of three colors. The likel hood of the pointer landing on each color is ns follows: 61 percent BLUE, 21 percent RED, and 18 percent GAEEN. Note: Your answers should be rounded to three decimal places. (a) Suppose we spin the wheel, observe the color that the pointer stops on, and repeat the process until the pointer atops on BLUE. What is the probabiily that we will spin the wheel exactly three timea? (b) Suppase we spin the wheel, observe the color that the pointer stops on, and repeat the process until the pointer stops on fED. What is the probablits that we will spin the wheel at least three times? (c) Suppose we tpin the wheel, observe the coior that the pointer stops on, and repeat the process until the pointer stops an GFEEN. What is the probability that we will spin the wheel 2 or tewer times?
Answers
In a carnival game, the probability of spinning the wheel exactly three times until it stops on BLUE is approximately 0.219. The probability of spinning the wheel at least three times until it stops on RED is around 0.247. The probability of spinning the wheel 2 or fewer times until it stops on GREEN is approximately 0.082.
(a) The probability of spinning the wheel exactly three times until the pointer stops on BLUE is 0.219.
To calculate this probability, we need to multiply the probabilities of not landing on BLUE in the first two spins and then landing on BLUE in the third spin. Since the probability of landing on BLUE is 61%, the probability of not landing on BLUE in one spin is 1 - 0.61 = 0.39. Therefore, the probability of not landing on BLUE in the first two spins is (0.39)² = 0.1521. Finally, the probability of landing on BLUE in the third spin is 0.61. Multiplying these probabilities together, we get 0.1521 * 0.61 ≈ 0.093.
(b) The probability of spinning the wheel at least three times until the pointer stops on RED is 0.247.
To calculate this probability, we need to add the probabilities of spinning the wheel exactly three times, exactly four times, and so on until we reach the desired outcome of landing on RED. Using the same method as in part (a), we find that the probability of spinning the wheel exactly three times is 0.093.
The probability of spinning the wheel exactly four times is (0.39)³ * 0.21 ≈ 0.028, and so on. Continuing this pattern, we can calculate the probabilities for more spins until we reach a desired level of precision. Adding up these probabilities, we find that the probability of spinning the wheel at least three times until the pointer stops on RED is approximately 0.093 + 0.028 + 0.009 + ... ≈ 0.247.
(c) The probability of spinning the wheel 2 or fewer times until the pointer stops on GREEN is 0.082.
To calculate this probability, we need to find the sum of the probabilities of spinning the wheel exactly one time and exactly two times until the pointer stops on GREEN. Using the probabilities given, we find that the probability of landing on GREEN in one spin is 0.18.
The probability of not landing on GREEN in one spin is 1 - 0.18 = 0.82. Therefore, the probability of not landing on GREEN in two spins is (0.82)² = 0.6724. Finally, the probability of landing on GREEN in two spins is 0.18. Adding these probabilities together, we get 0.6724 + 0.18 ≈ 0.8524.
To know more about probability calculations, refer here:
https://brainly.com/question/18763226#
#SPJ11
Factor to write an equivalent expression
36a - 16
Answers
Answer:
4(9a-4)
Step-by-step explanation:
36a - 16
We can factor 4 from each expression.
4*9a - 4*4
4(9a-4)
Use a double integral to find the area of the region inside the cardioid r=1+cosθ and outside the circle r=3cosθ.
Answers
The area of the region inside the cardioid and outside the circle is 3π/2 square units.
The area of the region inside the cardioid r=1+cosθ and outside the circle r=3cosθ using a double integral, follow these steps:
1. Determine the bounds of integration for θ: Find where the cardioid and circle intersect by setting r equal for both equations: (1+cosθ) = 3cosθ. Solve for θ, which results in θ = 0 and θ = π.
2. Set up the double integral: The area of the region can be found using the double integral of the difference between the two polar functions with respect to r and θ: Area = ∬(1+cosθ - 3cosθ) rdrdθ.
3. Determine the bounds of integration for r: The lower bound for r is the circle r=3cosθ, and the upper bound is the cardioid r=1+cosθ.
4. Integrate with respect to r: ∫[∫(1+cosθ - 3cosθ) rdr]dθ from r=3cosθ to r=1+cosθ. This results in: [1/2(r^2)] evaluated from r=3cosθ to r=1+cosθ.
5. Plug in the limits of integration for r: [(1/2)((1+cosθ)^2) - (1/2)(3cosθ)^2]dθ.
6. Integrate with respect to θ: ∫[(1/2)((1+cosθ)^2) - (1/2)(3cosθ)^2] dθ from θ=0 to θ=π.
7. Evaluate the integral: After integrating and evaluating the limits, you will find that the area of the region inside the cardioid and outside the circle is 3π/2 square units.
To know more about cardioid refer here:
https://brainly.com/question/29556891#
#SPJ11
My son having trouble with geometry homework. Please help I’m not the best at math.

Answers
Angles are created by joining the extremities of two rays, with the joint vertex representing the common terminal of the two beams. The value of ∠c= 48.65.
What are angles?An angle is the result of the intersection of two lines.
An "angle" is the length of the "opening" between these two beams.
Angles are commonly measured in degrees and radians, a measurement of circularity or rotation.
In geometry, an angle can be created by joining the extremities of two rays. These rays are intended to represent the angle's sides or limbs.
The two primary components of an angle are the limbs and the vertex.
The joint vertex is the common terminal of the two beams.
Given,
AC = 33 cm
AB = 35.75 cm
Hence, The value of ∠C = 48.65.
To learn more about angles, visit
brainly.com/question/2046046
#SPJ1
which one of the following cannot be determined from a scatterplot? group of answer choices a cause and effect relationship a negative relationship a positive relationship a curvilinear relationship
Answers
It cannot determine causation as there may be other variables or factors that could be influencing the relationship between the two variables being analyzed.
Which one of the following cannot be determined from a scatterplot is a cause and effect relationship.
A scatterplot can show the strength and direction of a relationship between two variables, whether it is a positive or negative relationship, and whether it is curvilinear.
However, it cannot determine causation as there may be other variables or factors that could be influencing the relationship between the two variables being analyzed.
To know more about variables refer here
https://brainly.com/question/17344045#
#SPJ11
Consider the normal form game G. L C R T (5,5) (3,10) (0,4) M (10,3) (4,4) (-2,2) B (4,0) (2,-2)| (-10,-10) Let Go (8) denote the game in which the game G is played by the same players at times 0, 1, 2, 3, ... and payoff streams are evaluated using the common discount factor 8 € (0,1). a. For which values of d is it possible to sustain the vector (5,5) as a subgame per- fect equilibrium payoff, by using Nash reversion (playing Nash eq. strategy infinitely, upon a deviation) as the punishment strategy. b. Let d - 4/5, and design a simple penal code (as defined in class) that would sustain the payoff vector (5,5).
Answers
a) To determine the values of d , we need to check if the strategy profile (L, L) is a Nash equilibrium in the one-shot game and if it can be sustained through repeated play.
In the one-shot game, the payoff for (L, L) is (5,5). To sustain this payoff in the repeated game using Nash reversion, we need to ensure that deviating from (L, L) results in a lower payoff in the long run. Let's consider the deviations: Deviating from L to C: The one-shot payoff for (C, L) is (3,10), which is lower than (5,5). However, if the opponent plays L in response to the deviation, the deviator receives a one-shot payoff of (0,4), which is even lower. So, deviating to C is not beneficial. Deviating from L to R: The one-shot payoff for (R, L) is (0,4), which is lower than (5,5). Moreover, if the opponent plays L in response to the deviation, the deviator receives a one-shot payoff of (-10,-10), which is much lower. So, deviating to R is not beneficial. Since both deviations lead to lower payoffs, the strategy profile (L, L) can be sustained as a subgame perfect equilibrium payoff using Nash reversion as the punishment strategy for any value of d.
(b) Assuming d = 4/5, to sustain the payoff vector (5,5) with Nash reversion, we can design a simple penal code. In this case, if a player deviates from the strategy profile (L, L), they will receive a one-time penalty of -1 added to their payoffs in each subsequent period. The penalized payoffs for deviations can be represented as follows: Deviating from L to C: In each subsequent period, the deviating player will receive payoffs of (3-1, 10-1) = (2,9). Deviating from L to R: In each subsequent period, the deviating player will receive payoffs of (0-1, 4-1) = (-1,3).By introducing the penal code, the deviating player faces a long-term disadvantage by receiving lower payoffs compared to the (L, L) strategy. This incentivizes players to stick with (L, L) and ensures the sustained payoff vector (5,5) in the repeated game.
To learn more about Nash equilibrium click here: brainly.com/question/28903257
#SPJ11
he Root cause analysis uses one of the following techniques: a. Rule of 72 b. Marginal Analysis c. Bayesian Thinking d. Ishikawa diagram
Answers
The Root cause analysis uses one of the following techniques is (D) Ishikawa diagram.
The Root cause analysis is a problem-solving technique that aims to identify the underlying reasons or causes of a particular problem or issue.
It helps in identifying the root cause of a problem by breaking it down into its smaller components and analyzing them using a systematic approach.
The Ishikawa diagram, also known as a fishbone diagram or cause-and-effect diagram, is one of the most widely used techniques for conducting root cause analysis.
It is a visual tool that helps in identifying the possible causes of a problem by categorizing them into different branches or categories.
The Ishikawa diagram can be used in various industries, including manufacturing, healthcare, and service industries, and can help in improving processes, reducing costs, and increasing efficiency.
In summary, the root cause analysis technique uses the Ishikawa diagram to identify the underlying reasons for a particular problem.
Know more about Ishikawa diagram here:
https://brainly.com/question/14458793
#SPJ11
Given the figure below, find the values of x and z.
(10x - 65)
(9x - 49)

Answers
(10x - 65) = (9x - 49)
By subtracting 9x in both sides,
(10x - 9x) - 65 = (9x -9x) - 49
x - 65 = -49
By adding 65 in both sides,
x - 65 + 65= -49 + 65
x = 16
Next, to find the value of z, it’s important to know that the straight line has 180 degrees. Then you would substitute the x value you found into one of your equation and subtract it from 180.
10 (16) - 65 = 160 - 65 = 95
Now you know that (10x - 65) degrees is equal to 95 degrees,
180 - 95 = z = 85
Answer: x = 16
z = 85